6.6. Heat air vessel

Fig. 6.6.1 Schematic overview of a heat air vessel

Supplier type

Type label	Description	Active
Heat Airvessel	Vertically positioned, prismatic (constant area), non-vented, isolated air vessel	No

6.6.1. Mathematical models

A vertical air vessel or air chamber without air inlet can be modelled by four equations. The first equation describes the behaviour of the enclosed air:

(6.6.1)\[P V^{k}=C\]

with:

Variable	Description	Units
P	absolute air pressure	N/m2
V	air volume	m3
k	Laplace coefficient	-
C	constant	Nm if k = 1

The Laplace coefficient depends on the thermodynamic behaviour of the air. Isothermal expansion is described by k = 1. Adiabatic expansion is described by k = 1.4.

The second equation governs the discharge Q (defined positive, when the flow is from the air vessel into the system) :

(6.6.2)\[Q=-A_{\mathrm{av}} \frac{d x_{\mathrm{f}}}{d t}\]

in which A_av denotes the storage surface and x_f the fluid level in the air chamber with respect to the global co-ordinate system. The minus sign indicates that the chamber supplies fluid to the system when the fluid level is decreasing in time.

In steady state the air vessel does not supply fluid. Hence in steady state the governing equation is:

(6.6.3)\[Q=0\]

The last equation (6.6.4) defines the temperature of the water in the air vessel. This air vessel model assumes that the vessel is thermally isolated, i.e. no heat is transferred to or from the outside world. The water in the air vessel is assumed to be mixed instantaneously (ideally mixed tank). Using an energy balance for the air vessel, the change of temperature can be expressed as a function of the energy inflow:

(6.6.4)\[\begin{split}\begin{cases} \rho c_p T \frac{dV}{dt} = \dot{m} c_p T_{in}, & \text{if } \dot{m} < 0 \\ \frac{dT}{dt} = 0, & \text{if } \dot{m} \geq 0 \end{cases}\end{split}\]

During outflow the temperature in the air vessel does not change, the outflow temperature is taken equal to the temperature in the air vessel.

6.6.2. Airvessel properties

6.6.2.1. Hydraulic specifications

Description	Input	SI-units	Remarks
Bottom level	real	[m]	See remarks
Top level	real	[m]	See remarks
Air quantity by	Fluid Level Air volume Constant C		See remarks
Initial fluid level	real	[m]	If ”air quantity by” = Fluid Level
Initial air volume	real	[m³]	If ”air quantity by” = Air volume
Initial C in P*V = C	real	[J]	If “air quantity by” = Constant C
Chamber area	real	[m2]
Laplace coefficient	real	[-]
Temperature at t = 0 [s]	real	[°C]

Remarks

The air volume and the fluid level in the airvessel are determined by either the initial fluid level, the initial air volume or the initial constant C. One quantity has to be given by the user, the other two quantities are calculated by Wanda.

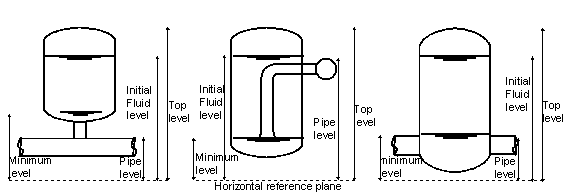
Fig. 6.6.2 Modelling assumptions per heat air vessel type.

An airvessel in WANDA is modelled with a straight instead of a rounded top and bottom. The volume of the real airvessel and the WANDA airvessel should be the same. The top and bottom level should therefore be taken respectively lower and higher than the level of the real airvessel. How much lower and higher depends on the shape of the real airvessel.

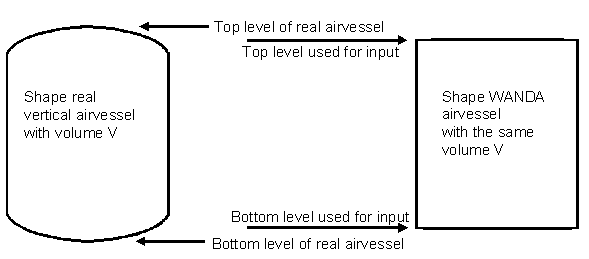
Fig. 6.6.3 Modeled heat air vessel versus real heat air vessel

Meaning of Pressure in property window Airvessel:

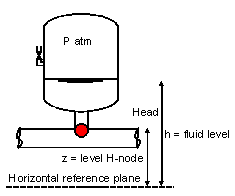
Fig. 6.6.4 Variables required for a heat air vessel

Variable	Description	Units
Head	Head in node of airvessel	m
Pressure P (in node)	\(\rho_l g (H - z)\) relative to the atmosphere	Pa
z	Height specified by a particular node	m
Air pressure (absolute)	\(\rho_a g (H-h) + P_{atm}\)	Pa
h	Fluid level	m

6.6.2.2. Component specific output

• Fluid level [m]

• Air pressure (absolute) [N/m².abs]

• Air volume [m³]

• Tank temperature [°C]

6.6.2.3. Component messages

Message	Type	Explanation
Top level below bottom level	Error	This is in input error by the user
Initial fluid level not in between top and bottom level of air chamber	Error	This is in input error by the user
Specified air volume larger than vessel volume	Error	This is in input error by the user
Empty airchamber	Warning	Computation can continue, since storage area is constant inde­pen­dent of the height. The results will not be physi­cally correct, but may help the design of the air vessel.
Airchamber refilled	Info	There has been a time with completely emptied air chamber, above.