6.13. Pump

Fig. 6.13.1 Schematic of a pump.

Fall type

Type label	Description	Active
incl. Heat	Complete pump model with various data and drives. Positive and negative speeds	yes

6.13.1. Mathematical model

A pump is not 100% efficient and therefore produces heat of which a fraction (fr) is transferred to the fluid. The temperature increase of the fluid is modelled as a quasi-steady process, thereby neglecting temporary heat accumulation effects in the pump housing. The fluid temperature increase is modelled by:

(6.13.1)\[\dot{m}c_{2}T_{2} = \dot{m}c_{1}T_{1} + fr\left( 1 - \eta \right)P\]

with:

variable	Description	Units
\(\dot{m}\)	Mass flow at duty point	kg/s
\(\eta\)	Pump efficiency at duty point	-
\(P\)	Pump shaft power	W
\(T_i\)	Temperature in the i-th heat node	K
\(c_i\)	Specific heat in the i-th heat node	K
\(fr\)	Fraction of generated heat absorbed by the fluid	-

The pump’s efficiency is determined every time-step from the pump curve (Q‑H and Q‑η). The pump data is supplied at a certain density. It is assumed that the pump curves remain valid over the entire range of temperatures and densities used in the calculation.

The remainder of this chapter is identical to the pump component described in the WANDA Liquid manual. The only difference is explained above and no additional information is included for the pump in WANDA Heat. Although the core variables have been changed (mass flow Instead of discharge, pressure Instead of head), the pump curves are still expressed in discharge, head and efficiency.

As the pump (QHE) curves as provided by the manufacturer are (normally) given in fluid head (H) and not in pressure, there is no need to ‘translate’ the curves to different densities if the actual fluid is different from the fluid used in the tests. The other (temperature dependent) fluid properties however most likely do have an effect on the pump performance (efficiency). This effect however is not proportional and therefore it is not included in the pump model. The validity of the pump curves is to be determined by the pump manufacturer.

6.13.1.1. Affinity rules

In the most general case a pump can operate in four QH-quadrants for N≥0 and in four QH‑quadrants for N<0. In WANDA, two pump models are distinguished:

1. Pump model limited to the N≥0 case, see section Section 6.13.1.2.

2. Complete pump model for all N (<0, =0 and >0), see section Section 6.13.1.3.

Basic equations

In the first quadrant for N>0 a running pump is characterised by the following functions:

(6.13.2)\[H = f\left( Q \right),N = N_{r}\]

(6.13.3)\[\eta = g\left( Q \right),N = N_{r}\]

with:

variable	Description	Units
\(H\)	Pump head	m
\(Q\)	Pump dishcarge	m3/s
\(\eta\)	Pump efficiency	-
\(N\)	Pump speed	RPM
\(N_r\)	Rated pump speed (i.e., where the f and g curves have been defined)	RPM

To describe a tripping pump the torque function must be defined:

(6.13.4)\[T = h(Q), N = N_r\]

Affinity rules are used to derive equations (6.13.2), (6.13.3), and (6.13.4) at other pump speeds N_i than the rated pump speed Nr:

(6.13.5)\[\frac{H(N_i)}{H(N_r)} = \left( \frac{N_i}{N_r}\right)\]

(6.13.6)\[\frac{Q(N_i)}{Q(N_r)} = \left( \frac{N_i}{N_r}\right)\]

(6.13.7)\[\frac{T(N_i)}{T(N_r)} = \left( \frac{N_i}{N_r}\right)^2\]

The affinity rules – also known as the homologous relations – are based on the assumption that the flow field and the accompanying pressure field are independent of the size of the pump as long as the shape (proportions) remain the same, and that also the efficiency does not change with the size of the pump.

A tripping pump is simulated with Newton’s second law as a rotating mass:

(6.13.8)\[T_{d}-T=I_{p} \frac{d N}{d t} \frac{2 \pi}{60}\]

in which \(T_d\) is the driving torque and \(T\) is the torque exerted by the fluid on the pump impeller. \(I_p\) denotes the polar mass moment of inertia [kg m²] of rotating mass (=motor + impeller + fluid). Note: sometimes the value GD2 (GeeDeeSquared) is used which is four times the Ip

If the pump operates at a steady speed during normal operation T_d = T. The driving torque (\(T_d\)) can suddenly be zero, due to for example a power failure (T_d = 0). In the event of a pump trip the decaying pump speed is calculated from:

(6.13.9)\[dN = -\frac{60}{2 \pi} \frac{T}{I_p} dt\]

The differential equation is solved using Euler’s method. The torque for N_i is derived with the affinity rules (eq. (6.13.5), (6.13.6), and (6.13.7)).

The torque (\(T_d\)) is deter­mined by the speed-torque relation (in tabular form) of the driving motor-gearbox combination during a pump start.

6.13.1.2. The pump model for N≥0 (QHE table)

The equations describing the discharge (eq. (6.13.2)) and the efficiency (eq. (6.13.3)) are usually unknown in algebraic form. A pump manufacturer normally provides the discharge (eq. (6.13.2)) and efficiency (eq. (6.13.3)) curves in a graphical form, which only specify the first quadrant for N = Nr. The graphical curves need to be transforemd to tables, such that at the start of the simulation the Q-H table and the Q-E table are known for Nr. The torque table can be derived using:

(6.13.10)\[T = \frac{\rho_f g Q H}{\eta N_r}\]

with:

Variable	Description	Units
\(\rho_f\)	Fluid density	kg/m3
\(Q\)	Pump dishcarge	m3/s
\(\eta\)	Pump efficiency	-
\(g\)	Gravitational acceleration	m/s2
\(N_r\)	Rated pump speed (i.e., where the f and g curves have been defined)	RPM

However, the functions H and T have to be known in the second and fourth quadrant to simulate a pump trip. To get the values outside the table range the tables are extended to the ‘left hand’ and ‘right hand’ side with so-called extrapolation parab­olas. These parabolas have the following general forms:

Q-H, right of the table range:

(6.13.11)\[\frac{H}{H_r} = A_h \left( \frac{Q}{Q_r} \right)^2 + B_h \left( \frac{Q}{Q_r} \right) + C_h\]

Q-H, left of the table range:

(6.13.12)\[\frac{H}{H_r} = D_h \left( \frac{Q}{Q_r} \right)^2 + E_h \left( \frac{Q}{Q_r} \right) + F_h\]

Q-T, right of the table range:

(6.13.13)\[\frac{T}{T_r} = A_t \left( \frac{Q}{Q_r} \right)^2 + B_t \left( \frac{Q}{Q_r} \right) + C_t\]

Q-T, left of the table range:

(6.13.14)\[\frac{T}{T_r} = D_t \left( \frac{Q}{Q_r} \right)^2 + E_t \left( \frac{Q}{Q_r} \right) + F_t\]

The parabolas are defined in dimensionless form, by dividing the H, T and Q curves with their rated values to Hr, Tr and Qr (i.e. the values in the maximum efficiency point (at the rated pump speed Nr)). The extrapolation coefficients A and D are derived in from empirical data as a function of the pump specific speed N_S (see table 1 to 4).

Table 1: A_H coefficients and derivatives versus the pump specific speed NS

\(N_s\)	\(A_h\)	\(dA_H/dN_S\)
10	-0.446	-0.004100
20	-0.487	-0.005075
50	-0.649	-0.007263
100	-1.068	-0.009730
150	-1.622	-0.008070
200	-1.875	0.004690
250	-1.153	0.014440

Table 2: D_H coefficients and derivatives versus the pump specific speed NS

\(N_s\)	\(D_h\)	\(dD_H/dN_S\)
10	0.566	0.005100
20	0.617	0.006400
50	0.822	0.009650
100	1.389	0.013480
150	2.170	0.007370
200	2.126	-0.009100
250	1.260	-0.017320

Table 3: A_T coefficients and derivatives versus the pump specific speed NS

\(N_s\)	\(A_T\)	\(dA_T/dN_S\)
10	-0.332	-0.003800
20	-0.370	-0.004675
50	-0.519	-0.007588
100	-0.977	-0.010660
150	-1.585	-0.006080
200	-1.585	0.008050
250	-0.780	0.016100

Table 4: D_T coefficients and derivatives versus the pump specific speed \(N_s\)

\(N_s\)	\(A_T\)	\(dD_T/dN_S\)
10	0.704	0.005800
20	0.762	0.007375
50	0.999	0.010050
100	1.566	0.011270
150	2.126	0.002140
200	1.780	-0.013450
250	0.781	-0.019980

The specific speed (\(N_s\)) of a pump is used to characteriste its type and is defined as:

(6.13.15)\[N_s = \frac{N_r\sqrt{Q_r}}{H_r^{\frac{2}{3}}\]

Low values (<50) indicate a centrifugal (or radial) type of pump and high values (>200) indicate an axial type of pump. Each pump has a specific N_spec, which usually is not equal to one of the tabulated values of N_S. Linear interpolation is used to obtain the values for each \(N_s\) as:

(6.13.16)\[A_H(N_{spec}) = A_H(N_s) + (N_{spec} - N_s) \frac{dA_H}{dN_s}\]

The same method is applied for the other empirical coefficients (i.e., DH, AT and DT). The remaining coefficients are determined as follows:

• BH and CH are calculated using the last two Q-H table points.

• EH and FH are calculated using the first two Q-H table points.

• ET and FT are calculated using the first two Q-T table points.

The BT and CT coefficients are determined with the following steps:

A. First, the intersection point between the \(\frac{H}{H_r}\) curve and the \(T = 0\) line is determined:

(6.13.17)\[\frac{H}{H_r} = A_H\left(\frac{Q}{Q_r}\right)^2 + C_H\]

(6.13.18)\[\frac{H}{H_r} = \phi \left(\frac{Q}{Q_r} \right)^2 \ \text{, at the } T = 0 \ \text{line}\]

The T=0 line describes the relation between H and Q when the pump speed is such that the pump exactly maintains a hydraulic torque T = 0. The coefficient φ = -0.3 is an empirically derived coefficient, which is assumed to be a constant and independent of the pump specific speed. However, the coefficient \(\phi\) varies in reality between about -0.1 and -0.4. The intersection of both curves defines the discharge Q_T0 for which T = 0.

B. B_T and C_T are determined from the last table point of the Q-T table and the discharge Q = Q_T0 for which T = 0.

Figure 1 shows an example of the extrapolation parabolas where Q_T0 = 3.52 (dimensionless!).

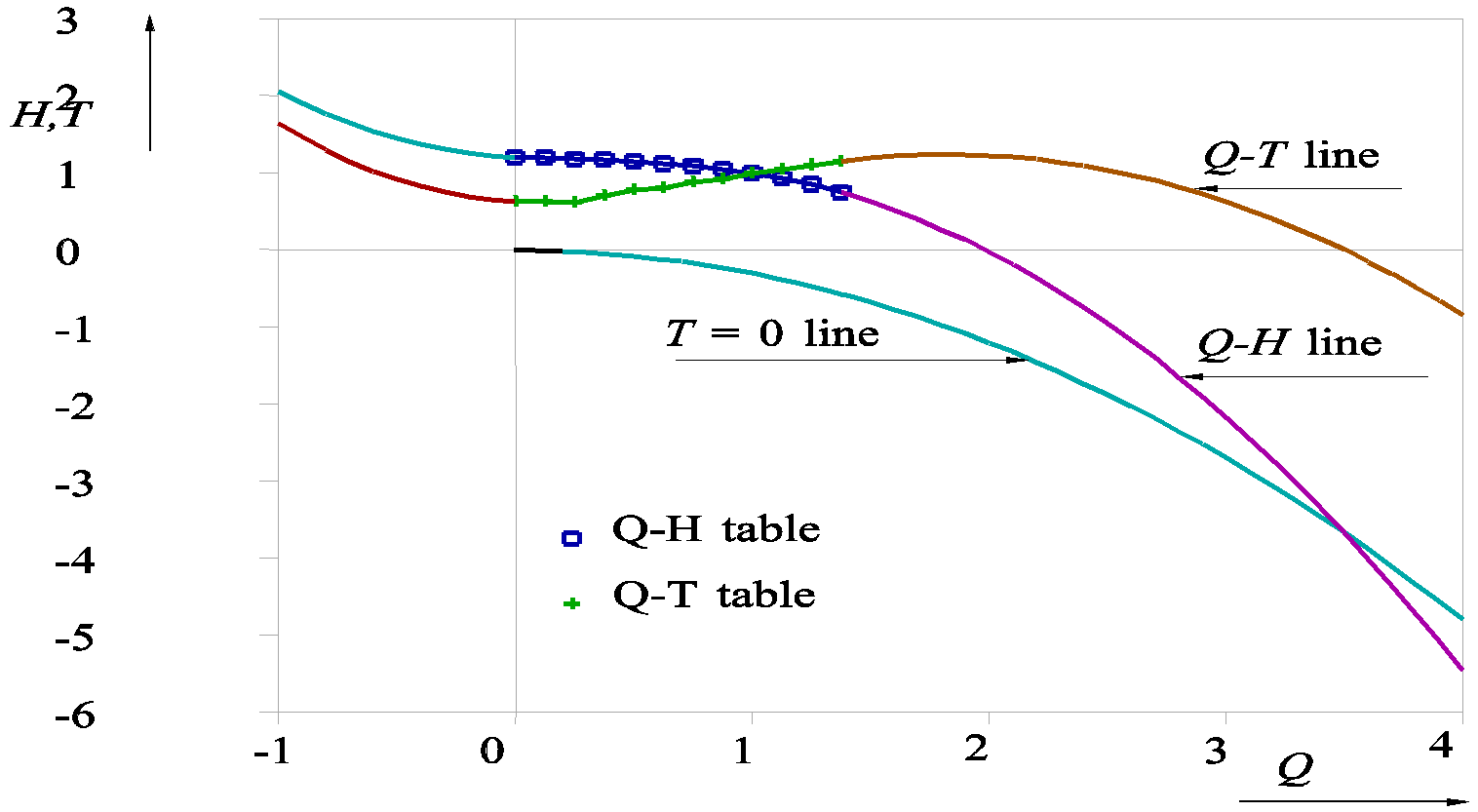
Fig. 6.13.2 Dimensionless curves of pump for N>0

6.13.1.3. The complete pump model (suter curve)

The heads and torque’s have to be measured and plotted as isolines in an N-Q graph for all combinations of Q and N (i.e., both positive and negative). In literature curves are defined for pumps of varying type (i.e., radial, mixed, and axial flow) at different specific speeds of 25, 147 and 261 (SI units), see for example Wylie, Fluid Transients in Systems, 1993.

The head, torque, discharge and speed are made non-dimesional by dividing the quantities by their respective values at rated (r) conditions.

(6.13.19)\[h = \frac{H}{H_{r}}\text{; }\beta = \frac{T}{T_{r}}\text{; } q = \frac{Q}{Q_{r}}\text{; } \alpha = \frac{N}{N_{r}}\]

Expressed in these dimensionless quantities the affinity laws read:

(6.13.20)\[\frac{h}{\alpha^{2}} \text{vs. }\frac{q}{\alpha}\text{; }\frac{\beta}{\alpha^{2}}\text{vs.}\frac{q}{\alpha}\text{; }\frac{h}{q^{2}}\text{vs.}\frac{\alpha}{q}\text{; }\frac{\beta}{q^{2}}\text{vs.}\frac{\alpha}{q}\]

These relations are difficult to handle from a computational point-of-view (dividing by zero when pump speed passes zero, and changing signs during transients). Marchand and Suter have overcome this difficulty by using:

(6.13.21)\[WH = \frac{h}{\alpha^{2} + q^{2}}\text{vs.}\tan^{- 1}\frac{q}{\alpha}\text{ and }\text{WB} = \frac{\beta}{\alpha^{2} + q^{2}}\text{vs.}\tan^{- 1}\frac{q}{\alpha}\]

A polar diagram of WH and WB can be plotted to obtain closed curves with pump data in all zones. Fig. 6.13.3 shows a polar diagram of WH and WB in a rectangular domain with\(\tan^{- 1}\left(\frac{q}{\alpha}\right)\) on the x-axis.

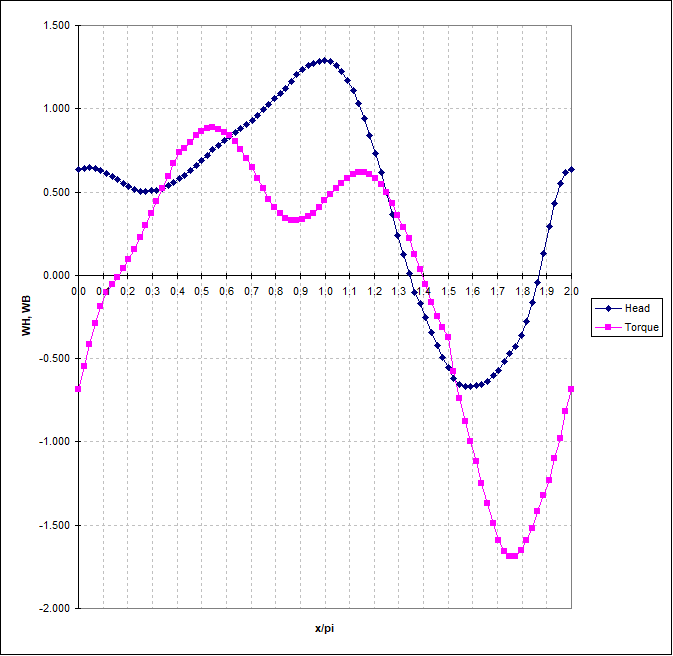
Fig. 6.13.3 Dimensionless Suter curves of radial pump (N_S=25, SI units)

The head and torque curves as function of discharge can be determined from the dimensionless Suter curves for any ratio of pump speeds (i.e., \(\alpha = N/N_r\)). Fig. 6.13.4 shows an example of a transformation from a Suter curve (i.e., Fig. 6.13.3) to a head and torque curve as function of discharge.

Fig. 6.13.4 Head and torque as function of discharge from the Suter curve shown in Fig. 6.13.3 for N>0.

This procedure works equally well for α < 0, α = 0 and α > 0. If a user selects the Suter characteristic type, the two transformation tables (i.e., WH(x) and WB(x)) are required. Additionally, the discharge, head and torque values at the best efficiency point are required. The WH/WB tables must be derived by manual transformation if the user only has access to a QHE-table. Gaps in the curves must be filled by interpolation from other known Suter curves at similar specific pump speeds (\(N_s\)). However, the results of the model calculation performed with interpolated curves must be interpreted with care, as the actual curves may deviate significantly.

6.13.1.4. Interpolation of the pump speed

The pump speed at t_new (= t_old + ∆t) is dereived from eq. (6.13.9) using integration with Euler’s method and sub-timesteps ∆t*:

(6.13.22)\[N_{\text{new}} = N_{\text{old}} + \frac{60}{2\pi}\frac{(T_d - T)_{(N_{\text{old}})}}{I_p}\Delta t\]

with:

Variable	Description	Units
\(N_{\text{new}}\)	Pump speed at \(t = t_{\text{new}}\)	RPM
\(N_{\text{old}}\)	Pump speed at \(t = t_{\text{old}}\)	RPM
\(T_d\)	Driving torque at \(t = t_{\text{old}}\)	Nm
\(T\)	Hydraulic torque at \(t = t_{\text{old}}\)	Nm

The maximum sub-timestep (\(\Delta t\)) during a pump trip (\(T_d = 0\)) is defined by Euler’s method. The maximum sub-timestep limits the variation between \(N_{new}\) and \(N_{old}\) (i.e., \(DN = N_{new} - N_{old}\)). Figure 4 illustrates the process of defining the value of \(DN_w\) (i.e., “wanted” DN). Figure 4 contains two regimes: \(DN_w\) is equal to \(DN = N_0 /100\) for \(N_{old} > N_0/10\) and \(DN_w\) is equal to \(DN = N_{old}/10\) for \(N_{old} \leq N_0/10\).

Figure 4: DN:sub:`w` as a function of N

The value \(N_{new}\) of is, at each time step, determined with the following procedure. An initial estimate of DN_w a new (sub) time step ∆t^* is determined as follows:

1. N_new is calculated using ∆t (first estimate)

2. The difference DN is calculated

3. Depending on N_old, DN_w is calculated (see figure 2)

4. The number of (sub) time steps within ∆t is calculated: N_t-steps = DN/DN_w

5. The new time step ∆t^* = ∆t/N_t-steps is calculated.

Finally, the N_new is calculated using ∆t^* (provided that N_t-steps > 1) until t = t_old ­+ ∆t.

6.13.1.5. Motor drive

The properties of a pump driven by a motor are presented below. The hydraulic torque (\(T\)) is a function of the drive torque (\(T_d\)):

(6.13.23)\[T_{d}-T=I_{p} \frac{d N}{d t} \frac{2 \pi}{60}\]

In general, when the motor is enabled, \(T_d = f(N, f_f)\) is a function of the pump speed (\(N\)) and the frequency (\(f_f\)) of the speed control. However, when the motor is disabled, a pump trip is simulated with \(T_d = 0\).

Typical speed-torque curves for electric motors (Fig. 6.13.5) and diesel engines (Fig. 6.13.6) are plotted below.

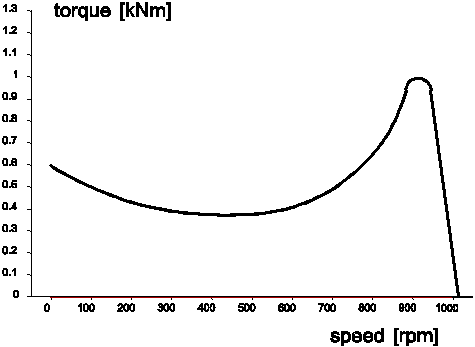
Fig. 6.13.5 Speed-torque curve for an electric motor

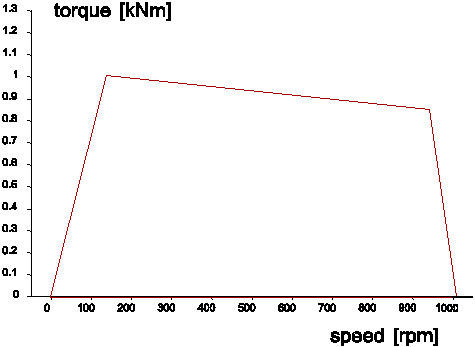
Fig. 6.13.6 Speed-torque curve for a diesel engine

A sharp drop (cut-off) is visible for poth pumps around their respective operating speed. Therefore, a higher torque (i.e., higher load) will not directly result in a change of the pump speed, which is also knwon as elastic behaviour. The steady-state speed of the pump is well-defined if the maximum torque just before the cut-off is sufficiently large. In steady state Wanda will compute two equilibria: 1) pump (QH) curve versus system resistance (QH relation) and 2) hydraulic torque versus motor torque. The head and torque both vary at each iteration step, which requires a specific iteration strategy to reach convergence of the numerical result.

The “synchronous speed” of an electric motor is the speed for which the torque passes through zero. Generally, the synchronous speed is 3000 RPM (i.e., the frequency of the AC power) divided by the number of coils, which is half the number of poles. In practice many two-coil (four pole) and three-coil (six pole) motors are used with their respective synchronous speeds of 1500 RPM and 1000 RPM. An electric motor can only generate torque if the shaft RPM exhibits a certain “slip” relative to the synchronous speed. The nominal power (and torque) will be delivered at somewhere between 1 and 3 % slip, where the slip value is specified by the manufacturer. The peak torque is about 3 times larger than the nominal torque. The start torque is about 2.2 times larger than the nominal torque and the sag torque (the relative minimum half way) is about 2 times the nominal torque.

The speed torque table has to be mirrored about the synchronous point to be able to “brake” or “force down” the pump by means of a temporarily negative torque. The speed torque table can be easily mirrored by adding the difference of the synchronous speed and the speed value to the synchronous speed and reversing the torque value of each speed-torque co-ordinate pair. Fig. 6.13.7 shows an example of a speed torque mirrored around the synchronous point.

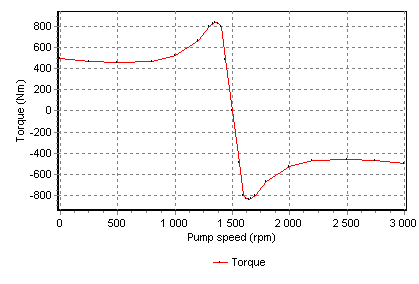
Fig. 6.13.7 Complete speed-torque curve for electric motor

The nominal power for the speed torque curve of Fig. 6.13.7 can be computed by multiplying the nominal torque (which could be 220 Nm) and the speed (which is in that case 155 rad/s), which results in a nominal power of 34.1 kW. However, this particaluar motor can also run at 150.8 rad/s (1440 RPM) delivering a torque of 490.7 Nm (this is the penultimate co-ordinate just before the synchronous point), which results in a power of 74 kW with a slip of 60 RPM. Whether this will lead to thermal problems depends on the design of the motor and that has to be confirmed by the manufacturer.

The speed values in the curve are offset by the relative frequency, thus moving the curve in horizontal direction, thereby also shifting the synchronous point to the left or right (decreasing or increasing of RPM). Theoretically the relative frequency can be zero but this will result in zero motor torque. In order to “force” the pump to lower RPM the speed-torque curve must also contain negative torque values for speeds greater than the synchronous speed.

In unsteady state the relative frequency should not be changed faster than the pump RPM can follow, otherwise the operating point (i.e., intersection between impeller speed-torque and motor speed-torque curves) will drop in the start-up zone.

6.13.2. Pump properties

6.13.2.1. Hydraulic specifications

Description	Input	SI-units	Remarks
Characteristic type	QHE Suter		Default = QHE
QHE_table	table		if Char. type = QHE
Suter table	table	Dim. less	if Char. type = Suter
Rated speed	real	[rad/s]
Q in best point of eff.	real	[m3/s]	if Char. type = Suter
H in best point of eff.	real	[m]	if Char. type = Suter
T in best point of eff.	real	[Nm]	if Char. type = Suter
Initial setting	Speed P_upstream P_downstream Mass flow Frequency		Default = Speed
Initial speed	real	[rad/s]	if Initial setting = Speed
Initial suction pressure	real	[N/m²]	if Initial setting = P_upstream
Initial discharge pressure	real	[N/m²]	if Initial setting = P_downstream
Initial mass flow	real	[kg/s]	if Initial setting = Mass flow
Initial relative frequency	real	[-]	if Initial setting = Frequency
Speed-Torque char.of motor	table		if Initial setting = Frequency
Polar moment of inertia	real	[kgm2]	only in transient mode
Drive type	Running Trip Speed Motorfreq Level OnOff		Default = Running
Trip time	real	[s]	if Drive type = Trip
Action table speed	table		if Drive type = Speed
Minimum speed for tripping	real	[rad/s]	if Drive type = Speed
Action table motorfreq	table		if Drive type = Motorfreq
Minimum rel.freq. for trip.	real	[-]	if Drive type = Motorfreq
Level On	real	[m]	if Drive type = OnOff
Level Off	real	[m]	if Drive type = OnOff
Start time (0 to max)	real	[s]	if Drive type = OnOff
Stop time (max to 0)	real	[s]	if Drive type = OnOff
Fraction gen. heat to fluid	real	[-]	1 (100%)

Because the Suter curves are dimensionless the discharge (Q), head (H) and torque (T) in the best efficiency point must also be supplied if the characteristic type is “Suter”.

In case of the QHE characteristic the Q and H at maximum efficiency will be found in the table. Hence the user must esure that there is only one maximum value within the E range.

Used table types

QHE table (Q to run from 0.0 upwards, H to decrease monotonously, E to be zero at either H=0.0 or Q=0.0)

Q [m3/s]	H [m]	E [-]
Real	Real	Real
Real	Real	Real

Suter table (x/π to run from 0.0 to 2.0)

\(x/\pi\) [-]	WH [-]	WB [-]
Real	Real	Real
Real	Real	Real

Three Suter curves from Wylie and 14 curves from Thorley have been included as property templates (see [installation dir]Property templatesExamplesSuter_pump)

Speed torque table in case of motor driven pump (see examples)

N [rad/s]	T [Nm]
Real	Real
Real	Real

Important:

• Minimum required rows is 5, maximum is 100.

• Efficiency must be specified dimensionless, not in percents: range 0 - 1 !

• The heads in the Q-H table must be monotonously decreasing.

• The Q-E table must have a maximum value for the efficiency E.

• Efficiency must be zero where either Q=0 or H=0.

• It is recommended to start QHE tables with Q = 0 [m3/s].

• The first and last row values of WH and WB should respectively have the same values (for x/π=0 and x/π=2), thus forming closed curves.

Steady-state settings

To determine the steady state condition of the pump the choice property “Initial setting” has to be set accordingly. The user has five choices:

Setting	Description
Speed	The operational speed is specified by the user. QH curve will be applied in computation and P1, P2 and Q are computed depending on system
P_upstream	The pressure upstream is specified by the user. P1 = C is applied in computation and P2 and Q are computed. Afterwards, the pump speed will be computed, such that the combination H2-H1 and Q is on the QH curve.
P_downstream	The pressure downstream is specified by the user. P2 = C is applied in computation and P2 and Q are computed. Afterwards, the pump speed will be computed, such that the combination H2-H1 and Q is on the QH curve.
Mass flow	The mass flow is specified by the user. \(\dot{m}\) = C is applied in computation and P1 and P2 are computed. Afterwards, the pump speed will be computed, such that the combination H2-H1 and Q is on the QH curve.
Frequency	The relative motor frequency is specified by the user. This is the actual frequency (e.g. 40 Hz) divided by the nominal frequency (e.g. 50 Hz) yielding the value of 0.8. With this relative frequency the speed-torque curve of the motor is adapted (shifted horizontally) and the steady state (P1, P2 and Q) will be solved such that motor torque and hydraulic (impeller) torque intersect. The point of intersection determines the actual pump speed.

Unsteady state settings

For the computation of the pump during unsteady state there are five possibilities to choose from in the property “Drive type”

Drive type	Description
Running	The pump speed and the QH curve will be kept constant, throughout the complete simulation time. Value for “polar moment of inertia” is not used
Trip	The pump speed and QH curve will be maintained until the user specified “trip time”. Thereafter the motor torque will be zero and the pump will trip according to equation (16).
Speed	The pump speed will be determined by applying the time-speed table (which is specified by the user). Polar moment of inertia is not taken into account during use of the table. If the value for ”min speed for tripping” has been undershoot, the speed table is overruled and the pump acts as a tripping pump, see remark 3.
Motorfreq	The pump speed will be computed by applying the transformed speed-torque curve of the motor on basis of the time table for the relative frequency (which is specified by the user)
Level OnOff	Fixed speed pump is switched on if upstream head H1 > “Level On”; speed increases in “Start time” seconds from 0 to “Rated speed” Pump is switched off if upstream head H1 < “Level Off”; speed decreases in “Stop time” seconds from rated speed to 0 Polar moment of inertia is not taken into account This pump type can be used for simple pump operation control; use a Control module for advanced operational control

Remark 1:

It is most logical to apply drive type “Speed” in combination with initial setting “Speed” and drive type “Motorfreq” in combination with initial setting “Frequency” in order to have a smooth transition between the steady state and unsteady state computations. However, different combinations are possible. The user must take care that the pump speeds match between steady and unsteady. Differences will however be solved dynamically: the unsteady state solution process aims at achieving a new balance.

Remark 2:

All “Drive type” types may be controlled by a control loop (C-components).

Remark 3:

To trigger the “trip” action at certain point in time T the minimum speed for tripping can be used. The table value of the speed just before T must be higher than this minimum speed and lower after T.

6.13.2.2. Component specific output

• Pump speed [rad/s]

• Fluid torque [Nm]

• Motor torque [Nm]

• On/Off [-]

• Efficiency [-]

• power [W]

• Energy [J]

6.13.2.3. Actions

How to activate the pump is dependent of the drive type:

Running

If the type is “running” there will be no action applicable. The pump just keeps running and the fixed QH-curve will apply throughout the computation. The speed may be overruled by a control connection (signal line).

Trip

If the drive type is “trip” the input value “trip time” will determine the time at which the driving torque becomes zero and the pump speed will solely be determined by the hydraulic torque. Up to the “trip time” the pump will be running at constant speed, although the speed may be overruled by a control connection (signal line).

Speed

If the drive type is “speed” the action table will be of the time-speed type. In case the initial control is also “speed” the user interface will copy the initial speed into the table. In other cases (init_P1, init_P2, init_Q and motor), the initial pump speed will be calculated by the computational core (STEADY) and it is the user’s responsibility to have the time-speed table starting with the same pump speed. A warning will be issued however in case of a discrepancy. The action table may be overruled by a control connection (signal line).

MotorFreq

If the drive type is “MotorFreq” the action table will be of the type “relative frequency” which is a dimensionless table. The percentage will be used to scale the motor speed-torque curve relative to the y-axis (the speed will be multiplied by the scaling factor) resulting in lower torque values. The action table may be overruled by a control connection (signal line).

Level On/Off

If the drive type is “Level On/Off” the pump acts as a start/stop pump if the upstream head over/undershoot the On/Off values specified. The speed increase/decrease is defined by the ramp parameters.

6.13.2.4. Component messages

Message	Type	Explanation
Pump specific speed = Real	Info	Small number (<40) denotes centrifugal pump, large number (>100) denotes axial pump.
Initial pump speed = Real [rpm]	Info
Starts	Info
Pump starting	Info
Tripping	Info
Pump stopping	Info
Q‑H curve not monotonously Decreasing	Warning	To prevent instability, the derivative of H(Q) must be negative.
Convergence between fluid and motor torque less accurate than 0.1 % Fluid torque = Real [kNm] Motor torque = Real [kNm]	Warning	This will lead to a further convergence process in transient, therefore we are not yet in a steady state.
Initial‑running status contradictive with control based running status	Warning	For example, according to the initial status the suction controlled pump is running, whereas the measured suction level is below the switch off level.
Unbalance exceeding rpm sensitivity fluid torque = Real Nm motor torque = Real Nm	Warning	Within the accuracy of pump speed computation, it was not possible to obtain balance between hydraulic and motor torques. The pump speed is correct however and the torque unbalance will settle during the following time steps (dynamics).
Initial value of action table does not coincide with initial value of pump speed.	Warning	A possibly unintended “jump” in the pump speed will occur upon starting the unsteady state computation.
Motor overloaded	Warning	The hydraulic torque has become larger than the maximum (peak) motor torque. The motor is not longer capable of holding the normal pump speed. This is called a powered trip.
Inconsistent pump speed between steady state results and control system; steady state value will be used	Warning	Message given if discrepancy between steady state speed and control value is less than 1 %
Pump efficiency must be zero if either Q=0 or H=0 in input and non‑zero elsewhere	Error	To have a finite torque, this is by definition.
Pump efficiency less than 0 or greater than 1	Error
Motor overloaded Fluid torque = Real [kNm] Max. motor torque = Real [kNm]	Error	The intersection between hydraulic and motor torque is at the left of the maximum motor torque.
Inconsistent pump speed between steady state results and control system; Modify input	Error	Message given if discrepancy between steady state speed and control value is more than 1 %
Maximum torque of motor not occurring at pump speed higher than 0.1% of rated pump speed	Error
Drive type=Motorfreq only in combination with Initial setting=Frequency	Error
Can’’t compute pump speed	Error
Pump table entries < 2	Error
Operating point left of QH-table’	Error
Polar mom. of inertia < 0	Error