5.27. MOVAVG

Purpose

Computes the moving average of the input signal. The supported moving averages include:

• Simple Moving Average (SMA)

• Cumulative Moving Average (CMA)

• Weighted Moving Average (WMA)

• Exponential Moving Average (EMA)

Procedure

The procedure used to calculate the average varies depending on the type of averaging specified:

Moving Average Method	Formula
Simple Moving Average	(5.27.1)\[\text{SM}A_{t} = \frac{x_{t} + x_{t - 1} + \cdots + x_{t - (n - 1)}}{n}\]
Cumulative Moving Average	\(\text{CM}A_{t} = \frac{x_{1} + \cdots x_{t}}{t}\)
Weighted Moving Average	(5.27.2)\[\text{WM}A_{t} = \frac{nx_{t} + \left( n - 1 \right)x_{t - 1} + \cdots + x_{t - (n - 1)}}{n + \left( n - 1 \right) + \cdots + 1}\]
Exponential Moving Average	(5.27.3)\[\text{EM}A_{t} = \alpha x_{t} + \left( 1 - \alpha \right)\text{EM}A_{t - 1}\]

where xt is the signal value at time step t, and n is the window size to be used for averaging. Note that the user specifies the window size in seconds, such that the averaging is not heavily influenced by the choice of time step size.

For the SMA and WMA methods a queue of size n will be used to store past input values. This queue is filled with the steady state value, so the user does not have to specify these values themselves.

To calculate the moving average for successive values, it is possible to make computation of the SMA, CMA and WMA faster by rewriting the formulas to use the average value calculated at the previous time step. This results in the following expressions, which have been used for the implementation in Wanda:

Moving Average Method	Implementation in Wanda
Simple Moving Average	(5.27.4)\[\text{SM}A_{t + 1} = SMA_{t} - \frac{x_{t - n}}{n} + \frac{x_{t + 1}}{n}\]
Cumulative Moving Average	\(\text{CM}A_{t + 1} = \frac{t \cdot \text{CM}A_{t} + x_{t + 1}}{t + 1}\)
Weighted Moving Average
Exponential Moving Average	Unchanged

Calculating the average for the current time step by using the values of the previous time step can result in cumulative errors, which is inherent to the usage of floating point numbers. By using a double precision accumulator it is possible to reduce these errors, while keeping the speed-up by using these recursive expressions.

Parameters

Parameter	input	unit	range	default	remarks
Window size	real	[s]	[Δt, 2000* Δt]	Δt	Only for Simple and Weighted Moving Averages.
Weight factor	real	-	[0..1]	1	Only for Exponential Moving Average.

Remarks

The user specified window size is limited to a maximum of 2000 times the time step due to memory constraints. Because the window size n and the input values x_t are discrete values, the queue size (i.e. effective window size) shall be rounded to the nearest integer.

Examples

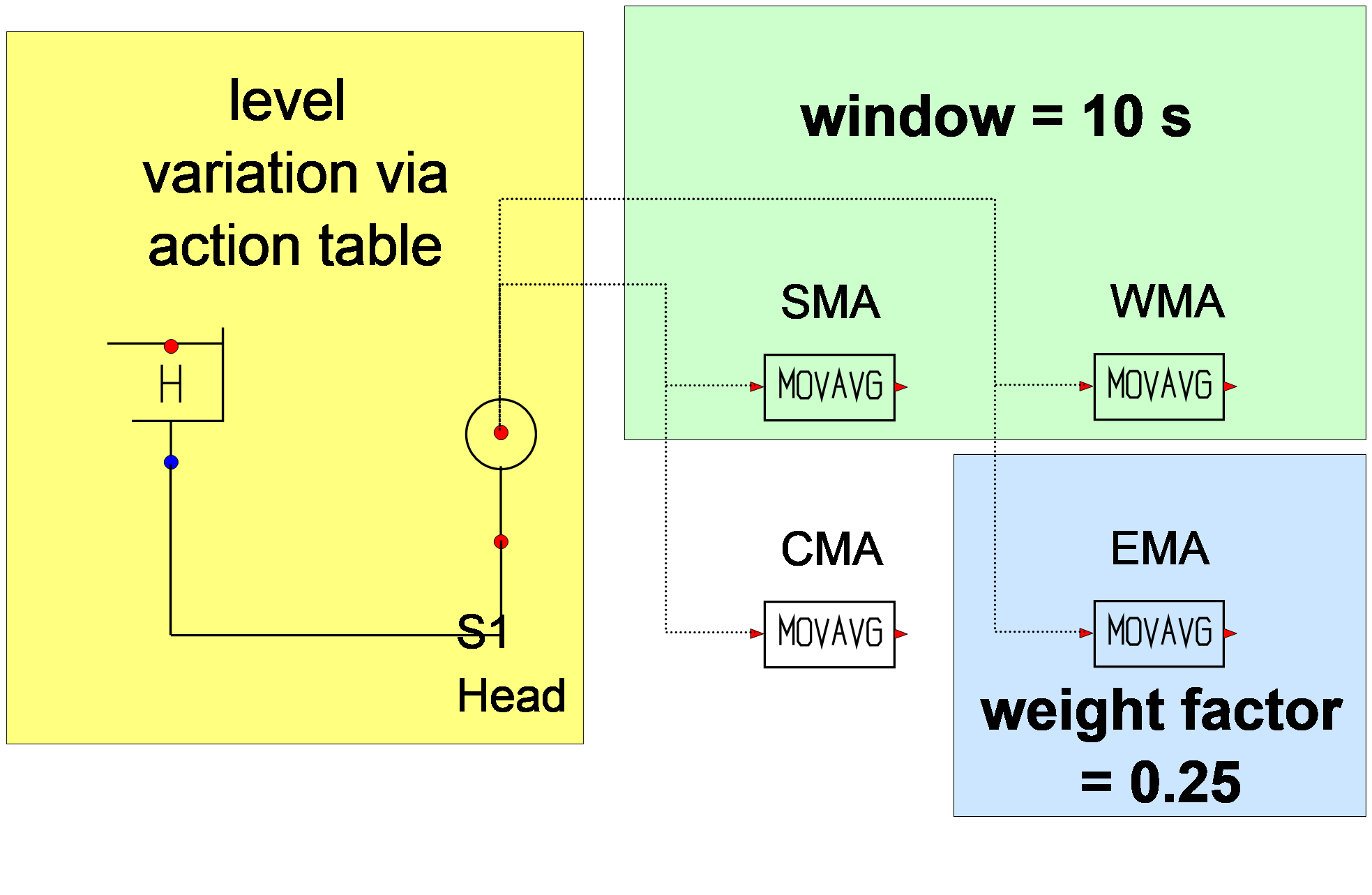
Fig. 5.27.1 Control scheme

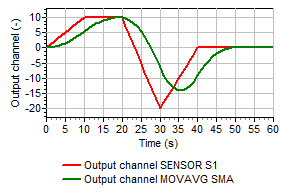
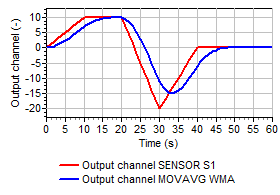
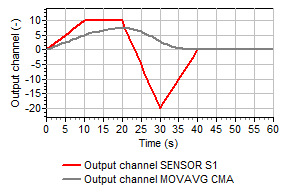
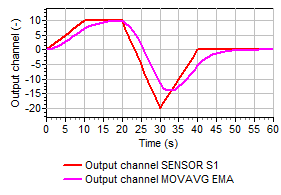
Figures 2a through 2d show the input and output of the various moving average methods.

Fig 2a: Input and output of a simple moving average with a window of 10 seconds.	Fig 2b Input and output of a weighted moving average with a window of 10 seconds.
Fig 2c: Input and output of a cumulative moving average.	Fig 2d: Input and output of an exponential moving average with a weight factor of 0.25.