5.33. PID_N

Purpose

To achieve a certain set value by adjusting a controlled variable of a hydraulic component, based on the difference between the input value and the set value. The PID_N component is similar to the PID component, except that the error can be normalized, as well as the output .

Procedure

The Proportional, Integrate, Differentiate Normalized (PID_N) component computes for each sample period Δt the error ε between an input signal x[n] and a set value xset:

(5.33.1)\[\varepsilon\left\lbrack n \right\rbrack = x\left\lbrack n \right\rbrack - x_{\text{set}}\]

where n denotes the present sample. This error is then normalized by the input lower bound and upper bound values:

(5.33.2)\[\varepsilon^{'} = \frac{\varepsilon}{x_{\text{upper}} - x_{\text{lower}}}\]

The unscaled output signal is computed by

Proportioning:

(5.33.3)\[y_{p}^{'}\left\lbrack n \right\rbrack = c_{p}\varepsilon^{'}\left\lbrack n \right\rbrack\]

Integrating:

(5.33.4)\[y_{i}^{'}\left\lbrack n \right\rbrack = y_{i}^{'}\left\lbrack n - 1 \right\rbrack + \frac{c_{p}}{c_{i}}\varepsilon^{'}\left\lbrack n \right\rbrack\text{Δt}\]

or Differentiating the normalized error:

(5.33.5)\[y_{d}^{'}\left\lbrack n \right\rbrack = c_{p}c_{d}\frac{\varepsilon^{'}\left\lbrack n \right\rbrack - \varepsilon^{'}\left\lbrack n - 1 \right\rbrack}{\text{Δt}}\]

where cp is the “gain”, ci is the “integration time constant”, cd is the “differentiation time constant”, Δt is the sample time-step and [n-1] denotes the previous sample. The equations above can be combined to give an unscaled output signal, which is either:

Proportional (P):

(5.33.6)\[y^{'} = y_{p}^{'} + c_{0}\]

Proportional and Integrated (PI):

(5.33.7)\[y^{'} = y_{p}^{'} + y_{i}^{'}\]

or Proportional, Integrated and Differentiated (PID):

(5.33.8)\[y^{'} = y_{p}^{'} + y_{i}^{'} + y_{d}^{'}\]

where c0 is an offset value. Finally, the scaled output signal is obtained using the output lower bound and upper bound values:

(5.33.9)\[y = y^{'}\left( y_{\text{upper}} - y_{\text{lower}} \right) + y_{\text{lower}}\]

Parameters

Parameter	input	unit	range	default	remarks
Initial setpoint	real				Can be overruled by 2nd input channel
Lower bound (input)	real
Upper bound (input)	real
Accuracy of recorded value	real				See remarks
Sample time interval	real	[s]			See remarks
Type of control	P/ PI/ PID
Gain	real
Integration time constant	real	[s]
Differentiation time constant	real	[s]
Offset value (bias)	real				only if ‘Type of Control” = P
Initial value of integrator	real				only if ‘Type of Control” = PI or PID Can be overruled by 3rd input channel
Lower bound	real
Upper bound	real
Ramp value CTRL_UP	real				max. positive change per second
Ramp value CTRL_DOWN	real				max. negative change per second

Remarks

The Sample time interval is used to decrease the resolution of the input signal. A PLC-controller can have a different sample time than the simulation time.

If the difference between the measured (recorded) value and setpoint is smaller than the accuracy, the error is set to zero.

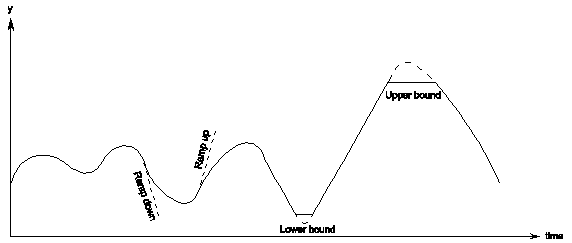
The PID component allows an ‘upper bound’ and a ‘lower bound’ to be imposed on the output signal.

When the output value “hits” the upper or lower bound the control system can not follow the error anymore and has no possibility to feed back to the system. If this situation remains long enough the integrator fills with a large value, which inhibits timely reaction if the error value changes direction (sign). To prevent this, a simple anti-reset windup provision is implemented. This provision suspends the accumulating of the error during the time that the output value violates the lower or upper bound.

Furthermore, a maximum allowable ‘ramp value’ can also be specified to control the rate of change of the output.

The integrating part can be initialised with a non-zero value. This can be used to adjust the PID controller to the hydraulic steady state (see examples).

In the steady state, the error should be equal to zero. This ensures that the entire system is in a true steady state.

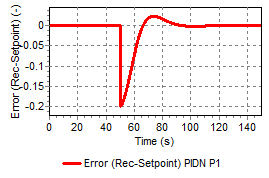
Figure 5: PID operation

It is the user’s responsibility to choose, and so that the output signal can be used by the controlled hydraulic component. For instance, if a valve is the controlled hydraulic component then the PID output signal must have a lower bound of 0 and an upper bound of 1.

Component Messages

Message	Explanation
Integrator must be less than upper bound	Input validation
Integrator must be greater than lower bound	Input validation
Offset must be less than upper bound	Input validation
Offset must be greater than lower bound	Input validation
Discrepancy with setpoint value and measured value
ERROR: Discrepancy with setpoint value more than 25 %	The control system and hydraulic system must be in equilibrium for the steady state, see remarks
Target below lowerbound, anti-reset windup provision activated	Informative
Target above lowerbound, anti-reset windup prov. de-activated	Informative
Target above upperbound, anti-reset windup provision activated	Informative
Target below upperbound, anti-reset windup prov. de-activated	Informative

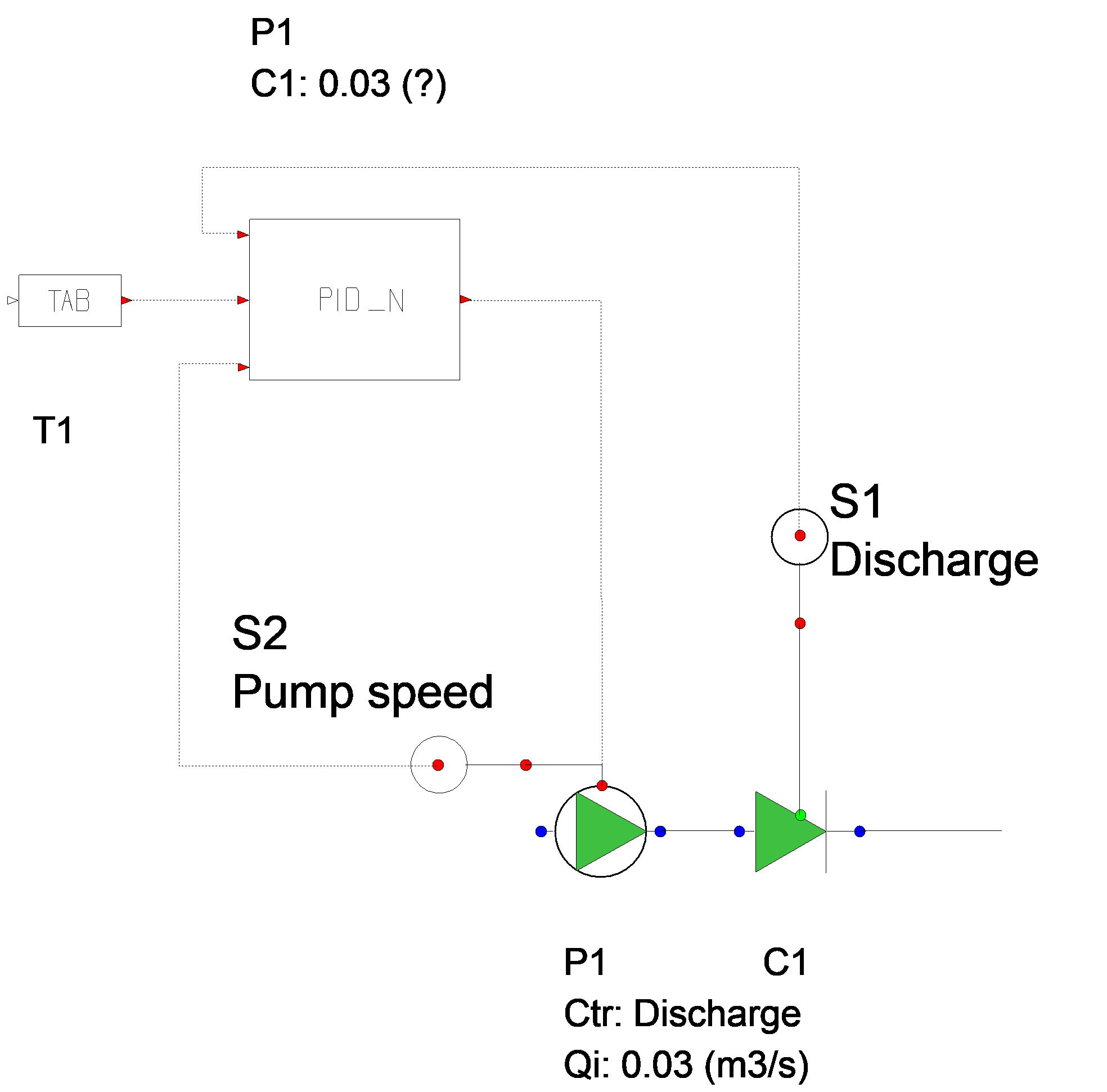
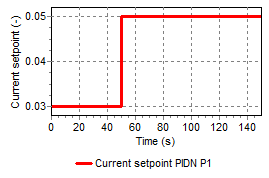
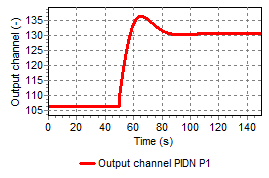
Examples