5.40. SFUN

Purpose

To transform an input signal . The transformation function can be either a sine-, polynome-, exponential- or power-function.

Procedure

One of the following functions is used to transform the input signal :

Sine	(5.40.1)\[y = A \cdot \sin\left( \text{Bx} - C \right)\]
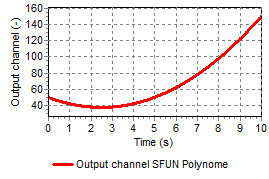
Polynome	(5.40.2)\[y = A + \left( B + Cx \right)x\]
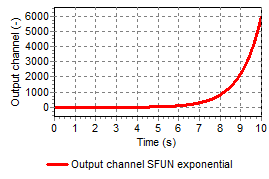
Exponential	(5.40.3)\[y = Ae^{\text{Bx} - C}\]
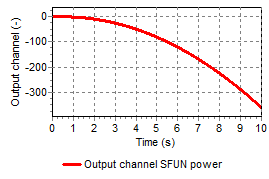
Power	(5.40.4)\[y = sign(Ax + B) \times abs(Ax + B)^{C}\]

Parameters

Parameter	input	unit	range	default	remarks
Function	Sine/ Polynome/ exp/ power
A	real
B	real
C	real

Remarks

The SFUN component is different from the FUN component, because the time itself is not used within the function. It will be obvious that if the input x is time-dependent, the output varies in time also.

Examples

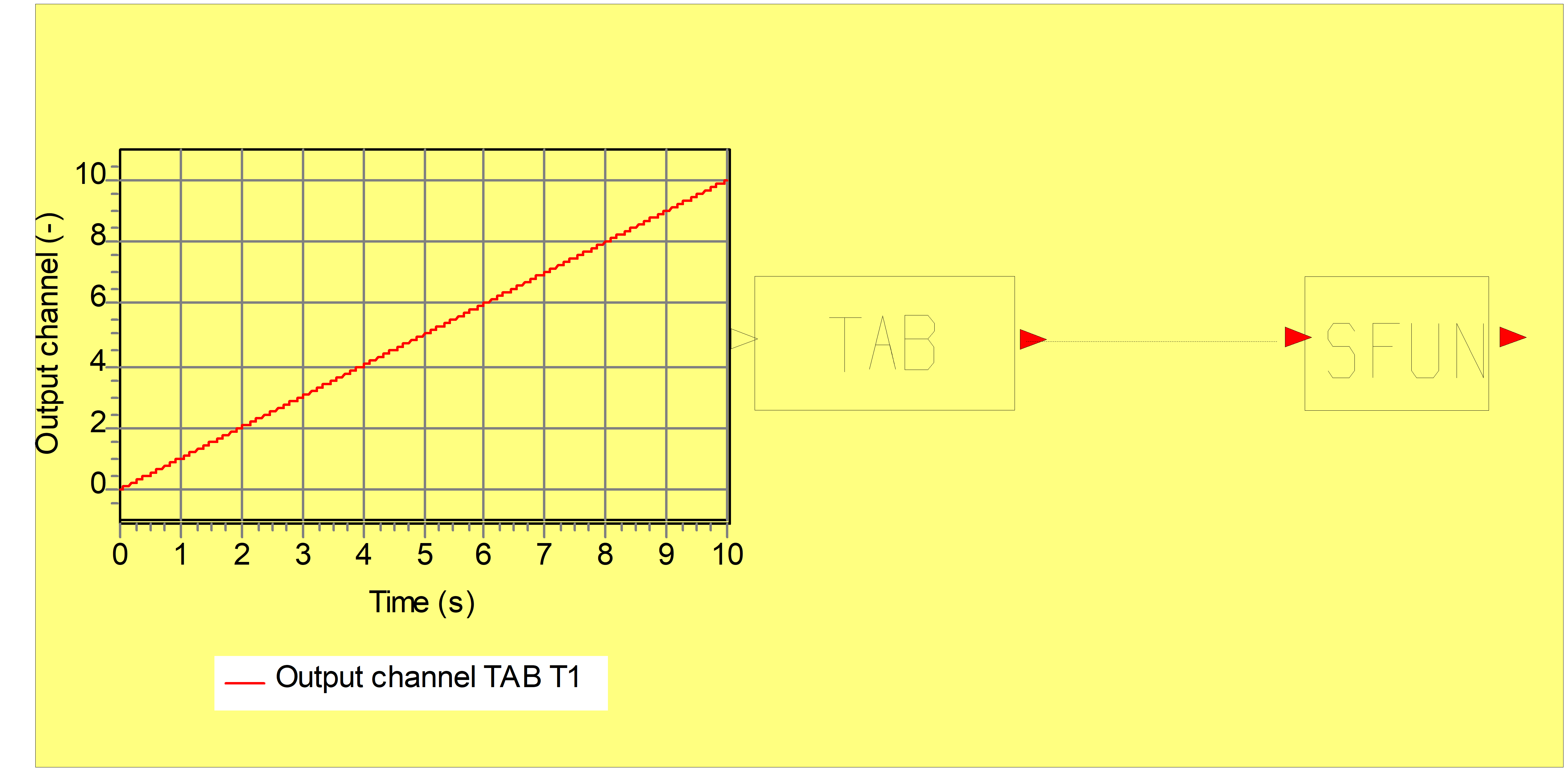
Fig. 5.40.1 Control Scheme

Figures 2a – 2d present output of different type of functions, where the input signal does vary with time (increasing from 0 – 10, see fig 1) and hence the output signals are also time-dependent.

Figure 2a:Sine signal (A= 2, B=1, C=2)	Figure 2b:Sine signal (A= 50, B=-10, C=2)

Figure 2c:Exponential signal (A= 2, B=1, C=2)	Figure 2d:Poweer signal (A= -20, B=1, C=2)