5.35. PIDSS_N

Purpose

To achieve a certain set value by adjusting a controlled variable of a hydraulic component, based on the difference between the input value and the set value. The PIDSS_N component includes an ON/OFF switch and is therefore similar to the PIDSS component, except that the error and output can be normalized. The component is mainly used for pump sumps in sewage systems.

Procedure

The Proportional, Integrate, Differentiate Start/Stop (PIDSS_N) component requires a minimum of two input signals: The first ‘input signal’ is used to compute the output signal. The second ‘switch value’ signal is used to determine whether to switch the PIDSS_N component ON or OFF.

The PIDSS_N component has four states: OFF, STARTING, ON and STOPPING (See Figure 4). Assuming the initial state is OFF, at the moment the input ‘switch value’ signal exceeds the ‘switch ON’ level, the state will change to STARTING. The output signal will then change linearly in time (bound by the ‘ramp value’) from the ‘output value when OFF’ to the ‘output start value’. The state then changes to ON.

During the first part of the ON state the output remains equal to the ‘output start value’ for a duration specified by the ‘stabilize time’. The second part of the ON state is the CONTROLLING part of the PIDSS_N component. If the input ‘switch value’ drops below the ‘switch OFF’ level the state will change to STOPPING. In this state the output value will decrease linearly from the ‘lower bound value’ to the ‘output value when OFF’, bound by the ‘ramp value’. Thereafter the state will revert to OFF.

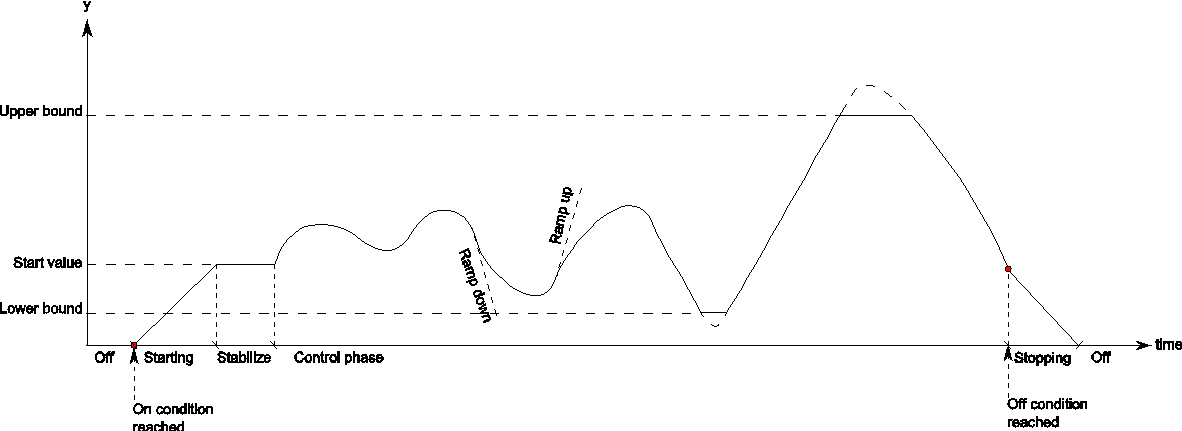
Figure 7: PIDSS_N operation

The Proportional, Integrate, Differentiate Normalized (PIDSS_N) component computes for each sample period Δt the error ε between an input signal x[n] and a set value xset:

(5.35.1)\[\varepsilon\left\lbrack n \right\rbrack = x\left\lbrack n \right\rbrack - x_{\text{set}}\]

and upper bound values:

(5.35.2)\[\varepsilon^{'} = \frac{\varepsilon}{x_{\text{upper}} - x_{\text{lower}}}\]

The unscaled output signal is computed by

Proportioning:

(5.35.3)\[y_{p}^{'}\left\lbrack n \right\rbrack = c_{p}\varepsilon^{'}\left\lbrack n \right\rbrack\]

Integrating:

(5.35.4)\[y_{i}^{'}\left\lbrack n \right\rbrack = y_{i}^{'}\left\lbrack n - 1 \right\rbrack + \frac{c_{p}}{c_{i}}\varepsilon^{'}\left\lbrack n \right\rbrack\text{Δt}\]

or Differentiating the normalized error:

(5.35.5)\[y_{d}^{'}\left\lbrack n \right\rbrack = c_{p}c_{d}\frac{\varepsilon^{'}\left\lbrack n \right\rbrack - \varepsilon^{'}\left\lbrack n - 1 \right\rbrack}{\text{Δt}}\]

where cp is the “gain” (whose units are determined by the units of the output signal), ci is the “integration time” (time units), cd is the “differentiation time” (time units), Δt is the sample time-step and [n-1] denotes the previous sample. The equations above can be combined to give an unscaled output signal, which is either:

Proportional (P):

(5.35.6)\[y^{'} = y_{p}^{'} + c_{0}\]

Proportional and Integrated (PI):

(5.35.7)\[y^{'} = y_{p}^{'} + y_{i}^{'}\]

or Proportional, Integrated and Differentiated (PID):

(5.35.8)\[y^{'} = y_{p}^{'} + y_{i}^{'} + y_{d}^{'}\]

where c0 is an offset value. Finally, the scaled output signal is obtained using the output lower bound and upper bound values:

(5.35.9)\[y = y^{'}\left( y_{\text{upper}} - y_{\text{lower}} \right) + y_{\text{lower}}\]

Parameters

Parameter	input	unit	range	default	remarks
input value to switch ON	real
input value to switch OFF	real
Reset time (on)	real	[s]
Reset time (off)	real	[s]
Initial status	ON/ OFF
Initial setpoint	real				Can be overruled by 3rd input channel
Lower Bound (input)	real
Upper Bound (input)	real
Accuracy of recorded value	real				See remarks
Sample time interval	real	[s]			See remarks
Type of control	P/ PI/ PID
Offset value (bias)	real				only if ‘Type of Control” = P
Gain	real
Integration time constant	real	[s]
Initial value of integrator	real				only if ‘Type of Control” = PI or PID Can be overruled by 4th input channel
Start value (output)	real
Use stabilize time		YES/ NO
Stabilization time	real				Only if “Use stabilize time” = YES
Lower bound (output)	real
Upper bound (output)	real
Ramp (max. change/sec)	constant/ variable
Ramp value	real				Only if Ramp = constant
Ramp value START	real				Only if Ramp = variable
Ramp value STOP	real				Only if Ramp = variable
Ramp value CTRL_UP	real				Only if Ramp = variable
Ramp value CTRL_DOWN	real				Only if Ramp = variable
Output value when OFF	real

Remarks

The Sample time interval is used to decrease the resolution of the input signal. A PLC-controller can have a different sample time than the simulation time.

If the difference between the measured (recorded) value and setpoint is smaller than the accuracy, the error is set to zero.

The PID component allows an ‘upper bound’ and a ‘lower bound’ to be imposed on the output signal.

When the output value “hits” the upper or lower bound the control system can not follow the error anymore and has no possibility to feed back to the system. If this situation remains long enough the integrator fills with a large value, which inhibits timely reaction if the error value changes direction (sign). To prevent this, a simple anti-reset windup provision is implemented. This provision suspends the accumulating of the error during the time that the output value violates the lower or upper bound.

Furthermore, a maximum allowable ‘ramp value’ can also be specified to control the rate of change of the output.

The integrating part can be initialised with a non-zero value. This can be used to adjust the PID controller to the hydraulic steady state (see examples).

In the steady state, the error should be equal to zero. This ensures that the entire system is in a true steady state.

It is the user’s responsibility to choose, and so that the output signal can be used by the controlled hydraulic component. For instance, if a valve is the controlled hydraulic component then the PID output signal must have a lower bound of 0 and an upper bound of 1. q

Component Messages

Message	Explanation
Integrator must be less than upper bound	Input validation
Integrator must be greater than lower bound	Input validation
Offset must be less than upper bound	Input validation
Offset must be greater than lower bound	Input validation
Discrepancy between initial state and on/off value	Switch value must be between (input) lower and upper bounds
ERROR: Discrepancy with setpoint value more than 25 %	The control system and hydraulic system must be in equilibrium for the steady state, see remarks
Discrepancy with setpoint value and measured value
Target below lowerbound, anti-reset windup provision activated	Informative
Target above lowerbound, anti-reset windup prov. de-activated	Informative
Target above upperbound, anti-reset windup provision activated	Informative
Target below upperbound, anti-reset windup prov. de-activated	Informative
change to Starting phase	Informative
change to Stabalize phase	Informative
change to Control phase	Informative
change to Off phase	Informative

Examples

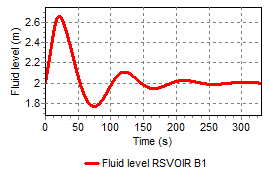
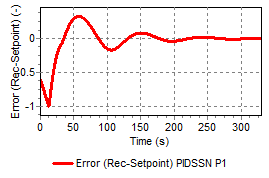
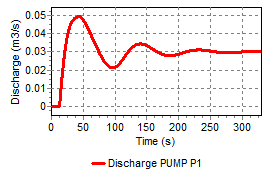
PID start/stop normalized component controlling discharge with a fluid-level dependent setpoint.