4.11. Damper, Surge vessel

4.11.1. Damper, Surge vessel

Fig. 4.11.1 Damper, Surge vessel (vertical bladdered)

Supplier type

Type label	description	active
Damper, Surge vessel	Vertically positioned, prismatic (constant area), bladder or piston type damper	No

4.11.1.1. Mathematical model

The damper or surge absorber is a vessel which allows for some dynamic (temporary) liquid storage upon exceedance of a certain (filling) pressure by compressing an enclosed gas volume. The gas is separated from the liquid by a bladder or a piston, to prevent it from being dissolved in the liquid. The damper described herein is a vertical, prismatic (e.g. a standing cylinder) vessel, with constant storage area.

If during the computation the system pressure exceeds the initial filling pressure, the behaviour of the vertical damper (or accumulator) is governed by two equations. The first equation describes the behaviour of the enclosed gas:

(4.11.1)\[P V^{k}=C\]

in which:

Variable	Description	Units
P	absolute gas pressure	N/m2
V	gas volume	m3
k	Laplace coefficient	‑
C	constant	Nm

The Laplace coefficient (also known as polytropic exponent) depends on the thermodynamic behaviour of the gas. Isothermal expansion is described by k = 1. Adiabatic expansion is described by k = 1.4 (for air or nitrogen). In the adiabatic case the polytropic exponent is the same as the isentropic exponent (κ), also known as the ratio of specific heats cp/cv. The gas is separated from the liquid by a bladder or a piston. The constant C is based on the filling pressure and the air volume of the damper with the bladder or piston fully down.

The second equation governs the amount of supplying discharge Q:

(4.11.2)\[Q=-A_{\mathrm{av}} \frac{d x_{\mathrm{f}}}{d t}\]

in which A_av denotes the storage surface and x_f the (effective) liquid level in the vessel with respect to the horizontal reference plane. The minus sign indicates that the vessel supplies fluid to the system when the fluid level is decreasing in time (thus a positive flow if supply to the system and a negative flow if supply to the vessel) in steady state and if the system pressure is below the initial filling pressure, the air vessel does not supply liquid. Hence in this state the governing equation is:

(4.11.3)\[Q=0\]

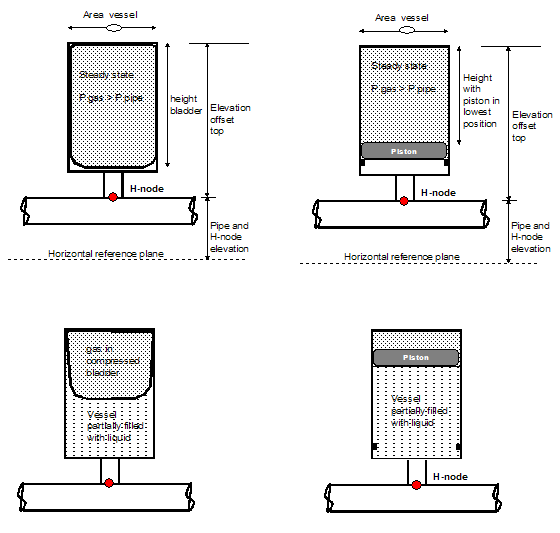
Fig. 4.11.2 Overview of surge vessels with a damper.

4.11.1.2. Hydraulic specifications

description	Input	unit	range	default	remarks
height	real	[m]			See remarks
area	real	[m2]	(0-100]		See remarks
elevation offset top	real	[m]			See remarks
filling pressure	real	[Pa]			Relative to atmospheric pressure
Laplace coefficient	real	[-]	[1-1.4]

Remarks

The initial gas volume: V_gas = height x area

The “elevation offset top” is introduced to use the same input parameters for differently located dampers. The real elevation of the top of the vessel is determined by:

Elevation top = elevation H-node + elevation offset top

Piston weight and friction and/or bladder tension are neglected

Inlet/outlet losses are not included in this damper model, but they can be easily taken into account by applying the additional component RESIST

4.11.1.3. Component specific output

Gas pressure [N/m².a] (Note: absolute pressure)

Gas volume [m³]

Fluid level [m]

Note

The default output parameters “Pressure” and “Pressure head” represent the P and H in the H-node of the Damper.