4.22. PUMPSS

4.22.1. PUMPSS (class)

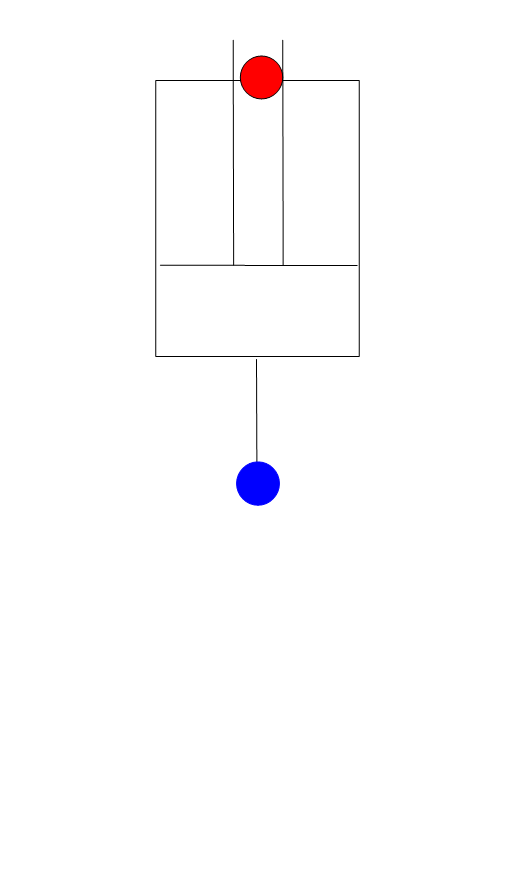
Fig. 4.22.1 Schematic of the Wanda Piston Pump component

Single cylinder, single-acting pump with mechanically driven piston

Supplier type

type label	description	active
Pump Simplex, single-acting	A single cylinder, with a mechanically driven single-acting piston..	Yes

A single cylinder reciprocating pump model can be created by connecting the cylinder to the node shared by two check valves in series See Figure 1.

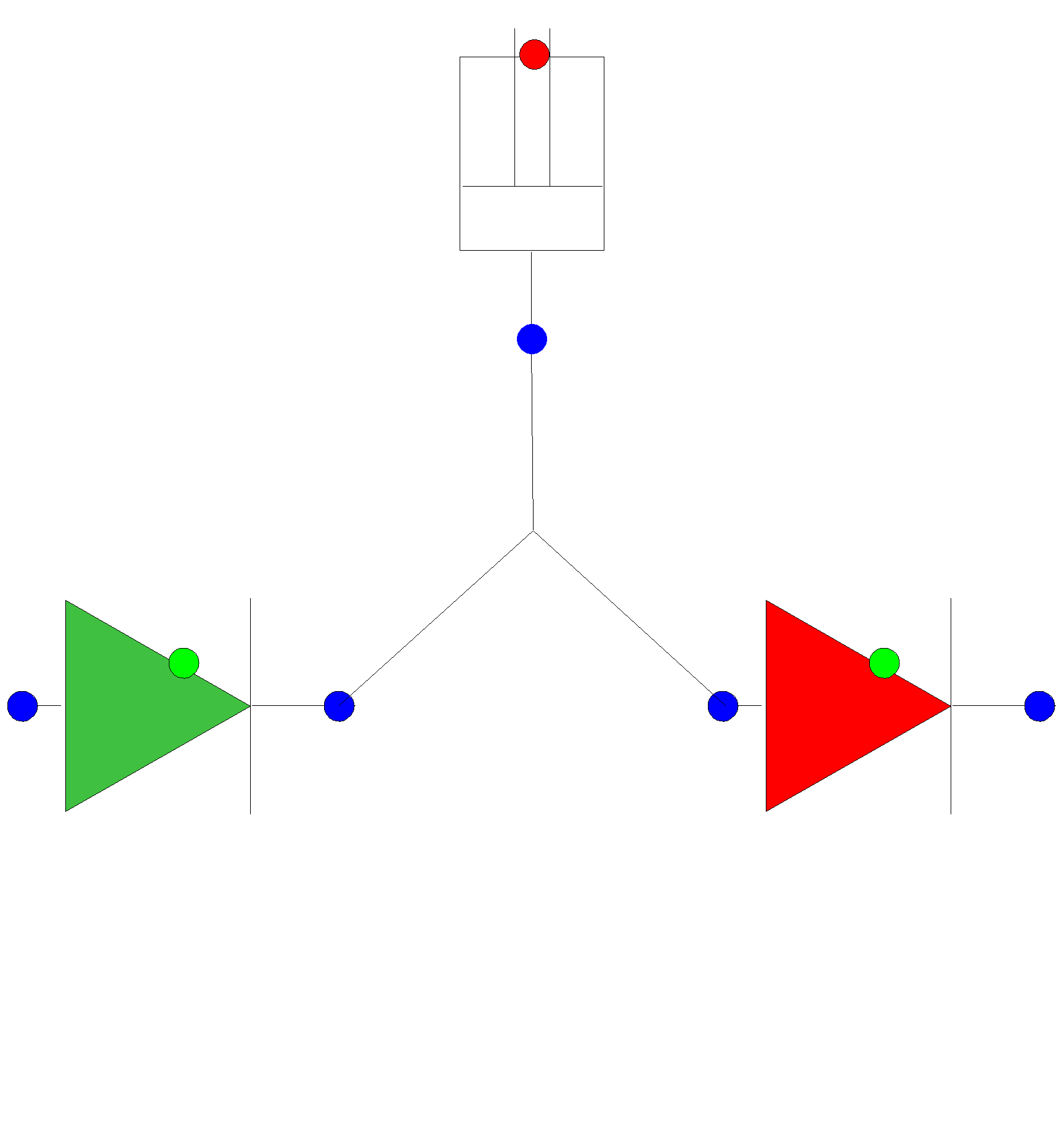
Fig. 4.22.2 Simplex, single-acting reciprocating pump model

A multi-cylinder pump model can be created by placing multiple instances of these cylinders and check valves in series

4.22.1.1. Mathematical model

Figure 2 shows the geometry of the one cylinder piston pump and its motion.

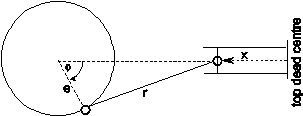
Fig. 4.22.3 Geometry of piston motion

The crank angle is defined as:

(4.22.1)\[\phi=\omega t+c\]

where Φ is the crank angle relative to the top dead centre (radians), ω is the constant pump speed (radians/sec), t is time and c is the crankshaft offset angle (radians). For a variable pump speed equation (4.22.1) can be rewritten as:

(4.22.2)\[\phi^{n}=\phi^{n-1}+\omega^{n} \Delta t\]

where n denotes the values of the present time-step, n-1 denotes the values of the previous time-step, Δt is the time-step length and x is the piston position relative to the top dead centre, e is the crank radius and r is the connecting rod length.

(4.22.3)\[x=e(1-\operatorname{Cos} \phi)+r\left(1-\sqrt{1-\left(\frac{e}{r} \operatorname{Sin} \phi\right)^{2}}\right)\]

The piston position may also be normalized [-1,+1] as:

(4.22.4)\[x_{n o r m}=\frac{x-e}{e}\]

The cylinder volume V and piston flow rate Qp (derived from the piston position) is given by:

(4.22.5)\[V=V_{T D C}+A_{p}\left[e(1-\operatorname{Cos} \phi)+r\left(1-\sqrt{1-\left(\frac{e}{r} \operatorname{Sin} \phi\right)^{2}}\right)\right]\]

(4.22.6)\[Q_{p}=-\omega A_{p} e \operatorname{Sin} \phi\left[1+\frac{e \operatorname{Cos} \phi}{r \sqrt{1-\left(\frac{e}{r} \operatorname{Sin} \phi\right)^{2}}}\right]\]

where VTDC is the cylinder volume at top dead centre and Ap is the piston area.

In the steady state there is no piston movement, hence no discharge is entering or leaving the cylinder. This can be written as a residual :

(4.22.7)\[Q=0\]

During motion the following continuity equation applies:

(4.22.8)\[Q=Q_{p}-\frac{d P}{d t} \frac{V}{K}\]

where Q is the discharge out of the cylinder, QP is the volumetric discharge of the piston, P is the pressure inside the cylinder and K is the bulk modulus of the fluid inside the cylinder. Dividing (4.22.8) by fluid density and gravity acceleration and integrating fully implicitly in time gives:

(4.22.9)\[F^{n}=H^{n}-H^{n-1}+\left(Q^{n}-Q_{p}^{n}\right) \frac{K \Delta t}{\rho g V^{n}}=0\]

Where H is the pressure head within the cylinder.

The piston pump model does not account for cavitation occurring within the pump cylinder.

4.22.2. PUMPSS (Piston Pump)

4.22.2.1. Hydraulic specifications

Description	input	unit	Range	default	remarks
Initial motor speed	Real	rad/s
Initial phase	Real	radians	0 - 2π	0
Cylinder volume	Real	m3			volume at top dead centre
Piston area	Real	m2
Crank radius	Real	m
Connecting rod length	Real	m

4.22.2.2. Component specific output

Motor speed [rad/s]

Piston position (normalized) [-]

Crank shaft angle [radians]

4.22.2.3. H-actions

Example:

To simulate a duplex, triplex or any other multicylinder pump, multiple instances of the PUMPSS component together with both checkvalves need to be placed parallel, with each cylinder having a unique phase angle.

The example below shows a triplex piston pump, with initial phase angle of respectively 0°, 120° and 240°.

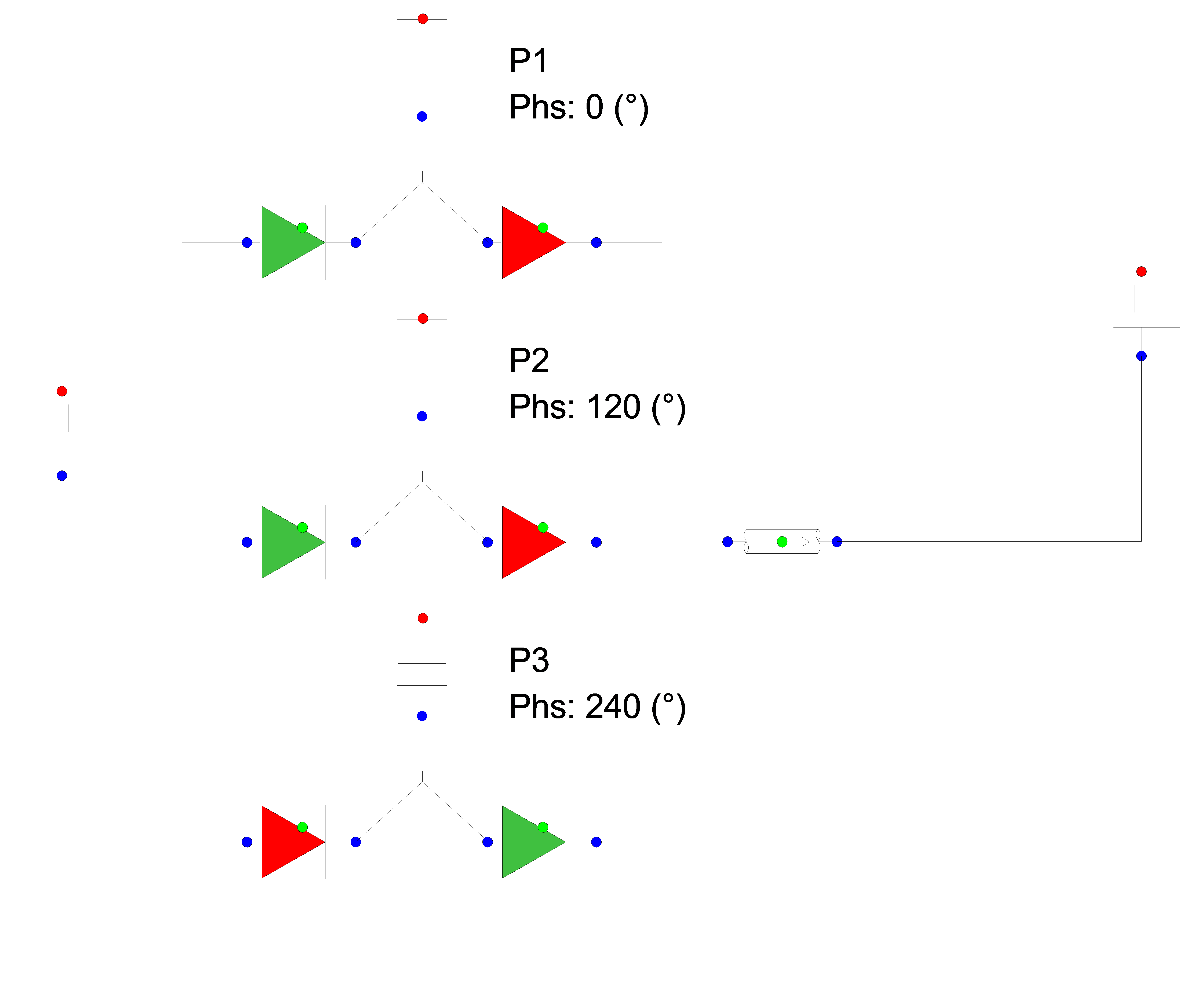
Fig. 4.22.4 Schematic overview of Wanda model

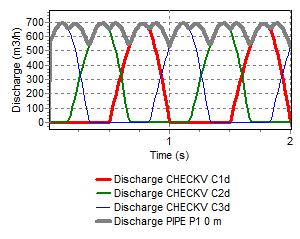
Fig. 4.22.5 Discharge of the modeled triplex piston pump.

4.22.2.4. Component messages

Message	Type	Explanation
Time-step should be smaller than reciprocating pump period	Error	Time-step is too large