4.19. Pressure relief valve

4.19.1. PRV (class)

Fig. 4.19.1 Pressure relief valve, safety valve

Fall type

Type label	description	active
PRV (Ideal)	This prv monitors the system pressure and opens upon exceedance of a set pressure. Opening time, friction, choking flow and valve dynamics are not taken into account.	No
PRV (simplified char.)	The opening pressure, as well as the full lift pressure and discharge, must be specified. (accumulation is taken into account).	No

4.19.1.1. Mathematical model

The PRV is always closed in the steady state. In steady state and closed state the governing equation of the prv component is very simple:

(4.19.1)\[Q_{1}=0\]

in which:

Variable	Description	Units
Q1	upstream discharge	m3/s

The PRV has been implemented as a Fall type (up- and downstream head and flow) to allow a downstream pressure that is different from atmospheric pressure. Only the PRV (simpl. char.) is influenced by the downstream pressure head.

If the system pressure (measured at the upstream H-node: H₁) exceeds the set pressure (gauge pressure) the prv opens, maintains the set pressure, P_set, and the governing equation of the ideal PRV becomes:

(4.19.2)\[H_{1}=\frac{P_{s e t}}{\rho_{f} g}+h\]

in which:

Variable	Description	Units
\(H1\)	pstream pressure head	m
\(Pset\)	set pressure (gauge)	N/m2
\(P_{f}\)	fluid density	kg/m3
\(g\)	gravitational acceleration	m/s2
\(h\)	elevation of PRV	m

The ideal PRV is not influenced by the downstream head, because it maintains the set pressure ideally.

In practice, however the PRV will not act ideally. The non-ideal behaviour can be modelled with a simplified characteristic of the PRV. After exceeding the set pressure the valve body will lift and gradually open upon increasing pressure and discharge. If the internal pressure keeps rising, the valve body will eventually hit a stop and the full lift condition is entered. From then on, the PRV will act as a resistance with constant loss coefficient. The simplified characteristic PRV is influenced by the downstream head so that the user may specify a boundary condition that is different from atmospheric pressure. One could think of a pressurised tank at the downstream side of the PRV.

In the partial lift phase ( 0 Q1 Qfull ) the governing equations are:

(4.19.3)\[\Delta P=\Delta P_{\mathrm{set}}+\left(\Delta P_{\mathrm{full}}-\Delta P_{\mathrm{set}}\right) \frac{Q_{1}}{Q_{\text {full }}}\]

(4.19.4)\[Q_{1}=Q_{2}\]

in which:

Variable	Description	Units
\(\Delta\) P	pressure difference over PRV: ρg ( H1 - H2 )	[N/m2]
\(\Delta\) Pset	set pressure difference	[N/m2]
\(\Delta\) Pfull	full lift pressure difference	[N/m2]
Qfull	full lift discharge	[m3/s]

In the full lift phase ( Q1 Qfull ) the governing equations are:

(4.19.5)\[\Delta P=\frac{\Delta P_{\text {full }}}{Q_{\text {full }}^{2}} Q_{1}^{2}\]

The Q P relation is shown in the figure below:

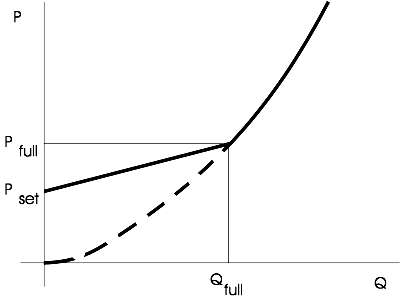
Fig. 4.19.2 Q-P relation for pressure relief valve (PRV)

The prv closes again if Q₁ < 0.

4.19.2. PRV (simplified char.)

4.19.2.1. Hydraulic specifications

Description	input	unit	range	default	remarks
set pressure (∆P)	real	[N/m2]	(0-108)
full lift pressure (∆P)	real	[N/m2]	(0-108)
full lift discharge	real	[m]	(0-108)

See also “Mathematical model” (Section 4.19.1.1).

Tip: The downstream head of the PRV should be set to the elevation level of the PRV if you want to model an atmospheric pressure at the downstream side.

4.19.2.2. Component specific output

None

4.19.2.3. H-actions

None

4.19.2.4. Component messages

Message	Type	Explanation
closes	Info
partially open	Info
fully open	Info

4.19.3. PRV (Ideal)

4.19.3.1. Hydraulic specifications

Description	Input	unit	range	default	remarks
set pressure (P upstr.)	Real	N/m2	(0-108)
Elevation	Real	m

See also “Mathematical model” (Section 4.19.1.1).

Tip:

The downstream head of the PRV should be set to the elevation level of the PRV if you want to model an atmospheric pressure at the downstream side.

4.19.3.2. Component specific output

None

4.19.3.3. H-actions

None

4.19.3.4. Component messages

Message	Message	explanation
Closes	Info
Opens	Info
Not valid (H2>H1), down­stre­am capacity exceed­ed	Warning	H2 does not play a role in the current mathematical model of the ideal prv. If however H2 becomes greater than H1 the prv “drowns” and effectively the computation loses physical relevance. This is a useful aid to design the downstream capacity.