4.40. Y-JUNCTION

Fig. 4.40.1 Schematic overview of Wanda Y-junctions

type label	description	active
Y-junction combining	Three-node junction with a non right angle branched leg and a combining flow. Both straight legs have the same diameter	no
Y-junction dividing	Three-node junction with a non right angle branched leg and a dividing flow. Both straight legs have the same diameter	no

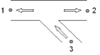
Both components can be used for all kind of flow regimes in a Y‑junction with several angles. The supported angles for the formula based types are 30, 45 and 60 degrees. The difference between the two Y-junctions has to do with the flow regime in the branched legs, combining either dividing. The arrows in the symbol specify the positive direction of the flow (and the velocity).

4.40.1. Mathematical model

4.40.1.1. Positive flow definition

The definition for the positive direction of flow (and velocity) is important to understand the results in the property window. Each Y-junction type has his own definition.

For the Y-junction combining component the positive flow definition is defined in the left figure below. For the Y-junction dividing component (right figure) the positive flow definition for the branch leg is opposite to that of the Y-junction combining. The positive flow definitions in the straight legs are the same for both types.

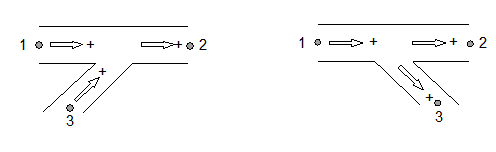
Fig. 4.40.2 Flow definitions for both types of Y-junction.

4.40.1.2. Flow regimes

In the table below all different flow regimes which can occur are listed and explained with a scheme with corresponding actual flow arrows. It is called straight flow if the total flow (in some literature also called: combined flow) is in one of the straight legs, branch flow means that the total flow is in the branch.

Table 4.40.1 definition of flow regimes for both types

	Y-junction combining type	Y-junction dividing type
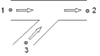
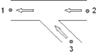
1 Combining straight flow	Positive straight flow	Negative straight flow
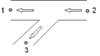
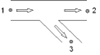
2 Dividing straight flow	Negative straight flow	Positive straight flow
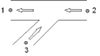
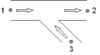
3 Combining straight flow	Negative straight flow	Positive straight flow
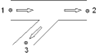
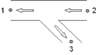
4 Dividing straight flow	Positive straight flow	Negative straight flow
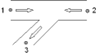
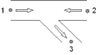
5 Combining branch flow	Negative branch flow	Positive branch flow
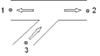
6 Dividing branch flow	Positive branch flow	Negative branch flow

4.40.1.3. Equations

The head loss over a 3-node component depends on the distribution of the discharges and the area of the connected legs. The Y-junction supports two different ways for retrieving the resistance coefficient Xi (ξ).

1. the head loss functions according to Idelchik’s Handbook [ref. 1] for angles of 30, 45 and 60 degree

2. user specified table with Xi depending on discharge ratio. These table values belong to a fixed area ratio.

Please note that the loss coefficients according to the handbooks apply to junctions with a certain minimum pipe length interval in between multiple junctions.

The head loss in 3-node components is a function of the combined flow in the combined leg, which is either one leg (1 or 2) of the straight part or the branch (leg 3). Including the continuity equation (no production or loss of mass in the component) the general set of the three equations of the Y-junction is:

(4.40.1)\[f_{1}=Q_{1}-Q_{2}+Q_{3}=0\]

ΔH Y-junction combining, combined flow in leg 2

(4.40.2)\[f_{2}=H_{1}-H_{2}-\xi_{12} \frac{Q_{2}\left|Q_{2}\right|}{2 g A_{2}^{2}}\]

ΔH Y-junction dividing, combined flow in leg 1

(4.40.3)\[f_{2}=H_{1}-H_{2}-\xi_{12} \frac{Q_{1}\left|Q_{1}\right|}{2 g A_{1}^{2}}\]

ΔH Y-junction, combined flow in branch

(4.40.4)\[f_{2}=H_{3}-H_{1}-\xi_{31} \frac{Q_{3}\left|Q_{3}\right|}{2 g A_{3}^{2}}\]

Where: Q _i = total discharge in leg i [m³/s]

H_i = energy head in connect point i [m]

A_i = pipe area leg i (leg with total flow) [m²]

ξ_ij = loss coefficient between point i and j [-]

The subscripts (1), (2) and (3) correspond to the different legs. The subscript x at the discharge Q_x refers always to the leg in which the combined (total) flow Q occurs.

For positive straight dividing flow and negative straight combining flow, Q₁ will be taken into account. For positive straight combining flow and negative straight dividing flow, Q₂ will be taken into account.

4.40.1.4. Resistance coefficients based on formulas

The resistance coefficients based of formulas are taken from the Idelchik Handbook with the following restriction to the section areas:

(4.40.5)\[\begin{split}\begin{array}{l} A_{1}+A_{3}>A_{2} \\ A_{1}=A_{2} \end{array}\end{split}\]

The formulas are only valid for the normal flow regimes 1 and 2, as explained in Table 4.40.1. For each formula the ξ‑values for various area and discharge ratios are collected in a table. Note that all indices used in the formulas are based on positive flow.

For the other flow regimes where one of the flow direction is around the acute angle there are no formulas available. For those situations a fixed value of ξ = 2,0 will be used.

Straight flow combining

For the straight leg, the resistance coefficient ξ₁₂ is calculated according to:

(4.40.6)\[\xi_{12} \approx 1-\left(1-\frac{Q_{3}}{Q_{2}}\right)^{2}-C_{\alpha} \frac{A_{2}}{A_{3}}\left(\frac{Q_{3}}{Q_{2}}\right)^{2}\]

Cα is a coefficient, which depends on the angle α. In WANDA three fixed α.values are included:

• α = 30°: Cα = 1,74;

• α = 45°: Cα = 1,41;

• α = 60°: Cα = 1,00.

Table Table 4.40.2, Table 4.40.3, and Table 4.40.4 shows the ξ₁₂ values according the formula above for various ratios of discharge and areas for the supported angles, respectively 30, 45 and 60 degrees.

Table 4.40.2 Values of ξ₁₂ for α=30° straight flow combining

		A3/A2
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q2	0.0	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	0.1	0.02	0.10	0.13	0.15	0.16	0.16	0.17	0.17	0.17	0.17
	0.2	-0.34	0.01	0.13	0.19	0.22	0.24	0.26	0.27	0.28	0.29
	0.3	-1.06	-0.27	-0.01	0.12	0.20	0.25	0.29	0.31	0.34	0.35
	0.4	-2.14	-0.75	-0.29	-0.06	0.08	0.18	0.24	0.29	0.33	0.36
	0.5	-3.60	-1.42	-0.70	-0.34	-0.12	0.03	0.13	0.21	0.27	0.31
	0.6	-5.42	-2.29	-1.25	-0.73	-0.41	-0.20	-0.05	0.06	0.14	0.21
	0.7	-7.62	-3.35	-1.93	-1.22	-0.80	-0.51	-0.31	-0.16	-0.04	0.06
	0.8	-10.18	-4.61	-2.75	-1.82	-1.27	-0.90	-0.63	-0.43	-0.28	-0.15
	0.9	-13.10	-6.06	-3.71	-2.53	-1.83	-1.36	-1.02	-0.77	-0.58	-0.42
	1.0	-16.40	-7.70	-4.80	-3.35	-2.48	-1.90	-1.49	-1.17	-0.93	-0.74

Table 4.40.3 Values of ξ₁₂ for α=45° straight flow combining

		A3/A2
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q2	0.0	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	0.1	0.05	0.12	0.14	0.15	0.16	0.17	0.17	0.17	0.17	0.18
	0.2	-0.20	0.08	0.17	0.22	0.25	0.27	0.28	0.29	0.30	0.30
	0.3	-0.76	-0.12	0.09	0.19	0.26	0.30	0.33	0.35	0.37	0.38
	0.4	-1.62	-0.49	-0.11	0.08	0.19	0.26	0.32	0.36	0.39	0.41
	0.5	-2.77	-1.01	-0.42	-0.13	0.05	0.16	0.25	0.31	0.36	0.40
	0.6	-4.24	-1.70	-0.85	-0.43	-0.18	-0.01	0.11	0.21	0.28	0.33
	0.7	-6.00	-2.54	-1.39	-0.82	-0.47	-0.24	-0.08	0.05	0.14	0.22
	0.8	-8.06	-3.55	-2.05	-1.30	-0.84	-0.54	-0.33	-0.17	-0.04	0.06
	0.9	-10.43	-4.72	-2.82	-1.87	-1.29	-0.91	-0.64	-0.44	-0.28	-0.15
	1.0	-13.10	-6.05	-3.70	-2.52	-1.82	-1.35	-1.01	-0.76	-0.57	-0.41

Table 4.40.4 Values of ξ₁₂ for α=60° straight flow combining

		A3/A2
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q2	0.0	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	0.1	0.09	0.14	0.16	0.17	0.17	0.17	0.18	0.18	0.18	0.18
	0.2	-0.04	0.16	0.23	0.26	0.28	0.29	0.30	0.31	0.32	0.32
	0.3	-0.39	0.06	0.21	0.28	0.33	0.36	0.38	0.40	0.41	0.42
	0.4	-0.96	-0.16	0.11	0.24	0.32	0.37	0.41	0.44	0.46	0.48
	0.5	-1.75	-0.50	-0.08	0.12	0.25	0.33	0.39	0.44	0.47	0.50
	0.6	-2.76	-0.96	-0.36	-0.06	0.12	0.24	0.33	0.39	0.44	0.48
	0.7	-3.99	-1.54	-0.72	-0.31	-0.07	0.09	0.21	0.30	0.37	0.42
	0.8	-5.44	-2.24	-1.17	-0.64	-0.32	-0.11	0.05	0.16	0.25	0.32
	0.9	-7.11	-3.06	-1.71	-1.03	-0.63	-0.36	-0.17	-0.02	0.09	0.18
	1.0	-9.00	-4.00	-2.33	-1.50	-1.00	-0.67	-0.43	-0.25	-0.11	0.00

For the branch leg. the resistance coefficient is calculated according to:

(4.40.7)\[\xi_{32}=A\left[1+\left(\frac{Q_{3}}{Q_{2}} \frac{A_{2}}{A_{3}}\right)^{2}-2\left(1-\frac{Q_{3}}{Q_{2}}\right)^{2}-C_{\alpha} \frac{A_{2}}{A_{3}}\left(\frac{Q_{3}}{Q_{2}}\right)^{2}\right]\]

The coefficient A depends on the area and discharge ratios again. Table 4.40.5 shows the values:

Table 4.40.5 Values of the variable A.

A3/A2	≤ 0.35	> 0.35
Q3/Q2	0.0 – 1.0	≤ 0.4	> 0.4
A	1.0	\(0.9\left(1-\frac{Q_{3}}{Q_{2}}\right)\)	0.55

Cα is a coefficient, which depends on the angle α. In WANDA three fixed α.values are included:

• α = 30°: Cα = 1.74;

• α = 45°: Cα = 1.41;

• α = 60°: Cα = 1.00.

Table Table 4.40.6, Table 4.40.7, and Table 4.40.8 shows the ξ₃₂ values according the formula above for various ratios of discharge and areas for the supported angles, respectively 30, 45 and 60 degrees.

Table 4.40.6 Values of ξ₃₂ for α=30° branch flow combining

		A3/A2
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q2	0.0	-1.00	-1.00	-1.00	-0.90	-0.90	-0.90	-0.90	-0.90	-0.90	-0.90
	0.1	0.21	-0.46	-0.57	-0.49	-0.50	-0.50	-0.51	-0.51	-0.51	-0.51
	0.2	3.02	0.37	-0.07	-0.15	-0.19	-0.21	-0.21	-0.22	-0.22	-0.22
	0.3	7.45	1.49	0.50	0.12	0.04	0.01	-0.01	-0.02	-0.03	-0.03
	0.4	13.50	2.89	1.13	0.32	0.20	0.14	0.11	0.10	0.09	0.09
	0.5	21.15	4.57	1.83	0.54	0.35	0.26	0.21	0.19	0.18	0.17
	0.6	30.42	6.55	2.59	0.75	0.48	0.35	0.29	0.25	0.24	0.23
	0.7	41.29	8.81	3.42	0.96	0.59	0.42	0.33	0.29	0.26	0.25
	0.8	53.78	11.35	4.32	1.17	0.69	0.46	0.35	0.29	0.26	0.25
	0.9	67.89	14.18	5.28	1.39	0.77	0.48	0.34	0.27	0.23	0.21
	1.0	83.60	17.30	6.31	1.60	0.84	0.48	0.31	0.21	0.17	0.14

Table 4.40.7 Values of ξ₃₂ for α=45° branch flow combining

		A3/A2
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q2	0.0	-1.00	-1.00	-1.00	-0.90	-0.90	-0.90	-0.90	-0.90	-0.90	-0.90
	0.1	0.24	-0.44	-0.56	-0.48	-0.49	-0.50	-0.50	-0.50	-0.50	-0.51
	0.2	3.16	0.44	-0.02	-0.12	-0.17	-0.19	-0.20	-0.21	-0.21	-0.21
	0.3	7.75	1.64	0.60	0.17	0.08	0.04	0.01	0.00	-0.01	-0.01
	0.4	14.02	3.15	1.31	0.39	0.25	0.19	0.15	0.13	0.12	0.12
	0.5	21.98	4.99	2.10	0.65	0.44	0.33	0.28	0.25	0.23	0.22
	0.6	31.60	7.14	2.99	0.91	0.61	0.46	0.38	0.33	0.31	0.29
	0.7	42.91	9.62	3.96	1.19	0.77	0.57	0.46	0.40	0.36	0.34
	0.8	55.90	12.41	5.02	1.47	0.92	0.66	0.52	0.44	0.39	0.36
	0.9	70.56	15.52	6.17	1.75	1.06	0.73	0.55	0.45	0.39	0.36
	1.0	86.90	18.95	7.41	2.05	1.20	0.79	0.56	0.44	0.37	0.32

Table 4.40.8 Values of ξ₃₂ for α=60° branch flow combining

		A3/A2
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q2	0	-1.00	-1.00	-1.00	-0.90	-0.90	-0.90	-0.90	-0.90	-0.90	-0.90
	0.1	0.28	-0.42	-0.54	-0.47	-0.49	-0.49	-0.50	-0.50	-0.50	-0.50
	0.2	3.32	0.52	0.03	-0.09	-0.14	-0.17	-0.18	-0.19	-0.20	-0.20
	0.3	8.12	1.82	0.72	0.23	0.13	0.08	0.05	0.03	0.02	0.01
	0.4	14.68	3.48	1.52	0.48	0.32	0.25	0.20	0.18	0.16	0.15
	0.5	23.00	5.50	2.44	0.79	0.55	0.43	0.36	0.32	0.29	0.28
	0.6	33.08	7.88	3.48	1.12	0.77	0.59	0.50	0.44	0.40	0.37
	0.7	44.92	10.62	4.63	1.46	0.99	0.75	0.62	0.54	0.48	0.45
	0.8	58.52	13.72	5.90	1.83	1.21	0.90	0.72	0.62	0.55	0.51
	0.9	73.88	17.18	7.28	2.21	1.43	1.03	0.81	0.68	0.59	0.54
	1.0	91.00	21.00	8.78	2.61	1.65	1.16	0.89	0.72	0.62	0.55

Straight flow dividing

For the straight leg the resistance coefficient is given using the following formula:

(4.40.8)\[\xi_{12}=\tau_{12} \frac{Q_{3}}{Q_{1}}\]

where τ₁₂ depends on the area and discharge ratios as given in table Table 4.40.9.

Table 4.40.9 Values of τ12

A3/A1	≤ 0.4	0.4
Q3/Q1	0-1.0	≤ 0.5	>0.5
τ12	0.4 (Q3/Q1)	0.2(2Q3/Q1 – 1)	0.3(2Q3/Q1 – 1)

Table 4.40.10 shows the ξ12 values according to the formula above for various values of discharge ratios.

Table 4.40.10 ξ₁₂ values for dividing flow

		A3/A1
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q1	0.0	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
	0.1	0.00	0.00	0.00	0.00	-0.02	-0.02	-0.02	-0.02	-0.02	-0.02
	0.2	0.02	0.02	0.02	0.02	-0.02	-0.02	-0.02	-0.02	-0.02	-0.02
	0.3	0.04	0.04	0.04	0.04	-0.02	-0.02	-0.02	-0.02	-0.02	-0.02
	0.4	0.06	0.06	0.06	0.06	-0.02	-0.02	-0.02	-0.02	-0.02	-0.02
	0.5	0.10	0.10	0.10	0.10	0.00	0.00	0.00	0.00	0.00	0.00
	0.6	0.14	0.14	0.14	0.14	0.04	0.04	0.04	0.04	0.04	0.04
	0.7	0.20	0.20	0.20	0.20	0.08	0.08	0.08	0.08	0.08	0.08
	0.8	0.26	0.26	0.26	0.26	0.14	0.14	0.14	0.14	0.14	0.14
	0.9	0.32	0.32	0.32	0.32	0.22	0.22	0.22	0.22	0.22	0.22
	1.0	0.40	0.40	0.40	0.40	0.30	0.30	0.30	0.30	0.30	0.30

The resistance coefficient ξ13for the branch is calculated using the following formula:

(4.40.9)\[\xi_{13}=A^{\prime}\left[1+\left(\frac{Q_{3}}{Q_{1}} \frac{A_{1}}{A_{3}}\right)^{2}-2\left(\frac{Q_{3}}{Q_{1}} \frac{A_{1}}{A_{3}}\right) \cos \alpha\right]\]

The values of A’ are given in Table 4.40.11.

Table 4.40.11 \(A'\) values for dividing flow

A3/A1	≤ 0.35	> 0.35
Q3/Q1	≤ 0.4	> 0.4	≤ 0.6	> 0.6
A’	1.1 – 0.7 Q3/Q1	0.85	1.0 – 0.65 Q3/Q1	0.6

Table Table 4.40.12. Table 4.40.13, and Table 4.40.14 shows the ξ13 values according to the formulas above for various values of discharge and area ratio for the supported angles of 30, 45, and 60 degrees.

Table 4.40.12 Values of ξ₁₃ for α=30° branch flow dividing

		A3/A1
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q1	0.0	1.10	1.10	1.10	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	0.1	0.28	0.40	0.55	0.59	0.65	0.69	0.72	0.75	0.77	0.78
	0.2	1.47	0.26	0.28	0.33	0.41	0.46	0.51	0.55	0.58	0.60
	0.3	4.28	0.58	0.24	0.21	0.26	0.31	0.36	0.40	0.43	0.46
	0.4	8.26	1.26	0.38	0.20	0.19	0.21	0.25	0.28	0.32	0.35
	0.5	14.74	2.48	0.76	0.27	0.18	0.17	0.18	0.21	0.23	0.26
	0.6	22.62	4.08	1.31	0.40	0.22	0.16	0.15	0.16	0.18	0.20
	0.7	32.19	6.11	2.04	0.62	0.32	0.20	0.16	0.15	0.15	0.17
	0.8	43.47	8.56	2.97	0.92	0.47	0.28	0.20	0.16	0.15	0.15
	0.9	56.45	11.44	4.08	1.30	0.67	0.39	0.26	0.19	0.16	0.15
	1.0	71.13	14.74	5.39	1.75	0.92	0.53	0.34	0.24	0.19	0.16

Table 4.40.13 Values of ξ₁₃ for α=45° branch flow dividing

		A3/A1
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q1	0.0	1.10	1.10	1.10	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	0.1	0.60	0.56	0.66	0.66	0.71	0.74	0.77	0.78	0.80	0.81
	0.2	2.08	0.56	0.48	0.47	0.52	0.56	0.59	0.62	0.64	0.66
	0.3	5.12	1.00	0.52	0.40	0.41	0.44	0.46	0.49	0.51	0.54
	0.4	9.30	1.78	0.73	0.43	0.38	0.37	0.38	0.40	0.42	0.44
	0.5	16.09	3.16	1.21	0.54	0.40	0.35	0.34	0.34	0.35	0.37
	0.6	24.24	4.89	1.85	0.69	0.45	0.36	0.32	0.31	0.31	0.31
	0.7	34.09	7.06	2.67	0.95	0.59	0.43	0.35	0.32	0.30	0.30
	0.8	45.63	9.64	3.69	1.30	0.78	0.54	0.41	0.35	0.32	0.31
	0.9	58.88	12.65	4.89	1.73	1.02	0.68	0.50	0.40	0.35	0.32
	1.0	73.83	16.09	6.29	2.23	1.30	0.85	0.61	0.48	0.40	0.35

Table 4.40.14 Values of ξ₁₃ for α=60° branch flow dividing

		A3/A1
		0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1.0
Q3/Q1	0.0	1.10	1.10	1.10	1.00	1.00	1.00	1.00	1.00	1.00	1.00
	0.1	1.03	0.77	0.80	0.76	0.79	0.81	0.82	0.83	0.84	0.85
	0.2	2.88	0.96	0.75	0.65	0.66	0.68	0.69	0.71	0.72	0.73
	0.3	6.23	1.56	0.89	0.65	0.61	0.60	0.61	0.62	0.63	0.64
	0.4	10.66	2.46	1.18	0.74	0.62	0.58	0.56	0.56	0.56	0.56
	0.5	17.85	4.04	1.79	0.89	0.68	0.58	0.54	0.52	0.51	0.51
	0.6	26.35	5.95	2.55	1.07	0.76	0.61	0.54	0.50	0.47	0.46
	0.7	36.55	8.29	3.49	1.39	0.94	0.72	0.60	0.53	0.50	0.47
	0.8	48.45	11.05	4.63	1.80	1.18	0.87	0.70	0.60	0.54	0.50
	0.9	62.05	14.24	5.95	2.29	1.46	1.05	0.82	0.68	0.60	0.55
	1.0	77.35	17.85	7.46	2.85	1.80	1.27	0.97	0.79	0.67	0.60

4.40.2. Y-Junction properties

The input properties of both Y-junction are exactly the same. The input and output properties for both types are specified below.

4.40.2.1. Properties Y-junction (combining and dividing type)

Input properties T-junction straight

Description	input	unit	range	default	Remarks
Diameter straight leg	Real	[mm]
Diameter branch leg	Real	[mm]
Xi method	Formula Tables			Formula
Xi tables valid for	Combining Dividing Both				Only when Xi method = Tables
Xi combining straight	Table (ξ12)				if Xi tables = Combining or Both
Xi combining branch	Table (ξ32)				if Xi tables = Combining or Both
Xi dividing straight	Table (ξ12)				if Xi tables = Dividing or Both
Xi dividing branch	Table (ξ13)				if Xi tables = Dividing or Both

With the tables for the Xi-values it is possible to choose user-defined loss coefficients. for instance for a certain kind of Y-junction with rounded angles. The user has to specify a set of loss coefficient values related to the discharge ratio between the branch leg and the straight combined flow leg. If the user does not specify both combining and dividing Xi-tables, WANDA uses the formulas according to the Idelchik handbook for the unspecified flow regimes.

Example of Xi table; straight flow combining, branch leg (ξ₃₂)

valid for Area ratio = 0.5

Discharge ratio [-]	Xi [-]
0.0	0.90
0.2	0.12
0.4	0.39
0.6	0.92
0.8	1.48
1.0	2.08

Component specific output Y-junction straight

Loss coefficient straight [-]	The ξ12 for positive flow and ξ21 for negative flow In case of branch flow regime this is the ξ31 coefficient
Loss coefficient branch [-]	The ξ13 for positive flow and ξ31 for negative flow In case of branch flow regime this is the ξ32 coefficient
Head loss straight [m]	The ΔH12 for positive flow and ΔH21 for negative flow In case of branch flow regime this is the ΔH13 for combining and ΔH31 for dividing flow
Head loss branch [m]	The ΔH13 for positive flow and ΔH31 for negative flow In case of branch flow regime this is the ΔH23 for combining and ΔH32 for dividing flow

Component messages Y-junction straight

Message	Type	Explanation
Combining	Info	Positive straight flow	Negative straight flow
Dividing	Info	Positive straight flow	Negative straight flow
Branch combining	Info	Positive branch flow	Negative branch flow
Branch dividing	Info	Positive branch flow	Negative branch flow

With the tables for the Xi-values it is possible to choose user-defined loss coefficients, for instance for a certain kind of T-junction with rounded angles. The user has to specify a set of loss coefficients values related to the discharge ratio between the side and combined branch. If the user does not specify both combining and dividing Xi-tables, WANDA uses the formulas according to the Idelchik handbook for the unspecified flow regimes.

NOTE: The numbering of the branches in the literature is not always consistent with the WANDA definition as given under ‘Mathematical Model’ above. The Miller Handbook for instance indicates the side branch with 1, the straight branch with 2 and the combined one as 3.