4.38. Weir

4.38.1. WEIR (class)

Fig. 4.38.1 Weir

Fall type

type label	description	active
WEIR (two way)	Broad crested weir, capable of simulating discharge in positive direction and negative direction.	No

4.38.1.1. Mathematical model

The component weir is often used in sewage water systems. The WEIR can have a discharge in positive or negative direction or can be closed. If the upstream head, H1, is larger than the downstream head, H2, then the WEIR will have a discharge in positive direction.

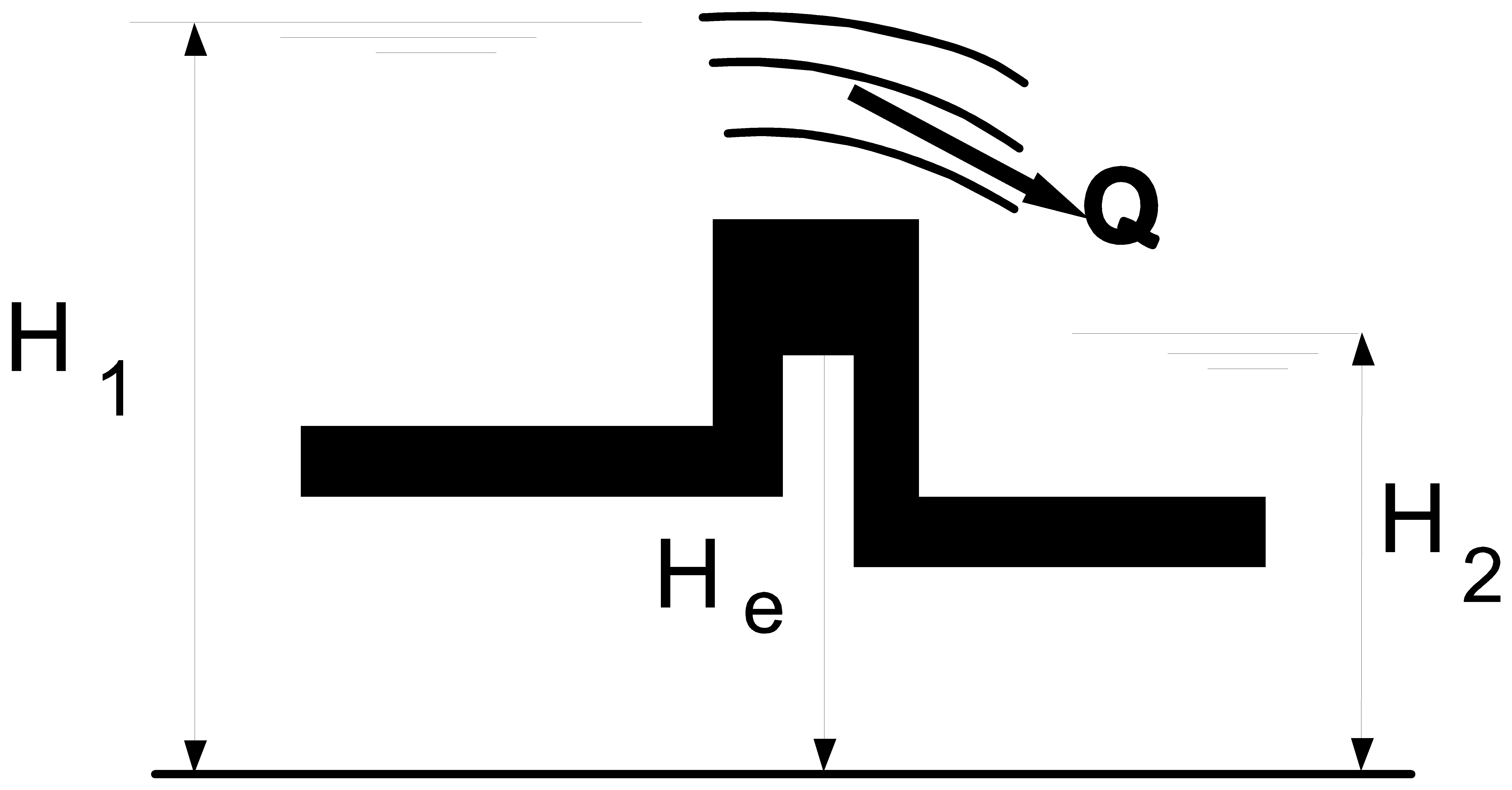
Fig. 4.38.2 Critical flow over a weir

The component can be modelled by the following equations if the flow over the edge is critical (Fig. 4.38.2):

(4.38.1)\[\begin{split}\begin{aligned} F_1 : Q &=\left(\frac{2}{3}\right)^{1,5} \sqrt{g} B C\left(H_{1}-H_{e}\right)^{1,5} \\ & \approx 1,7 B C\left(H_{1}-H_{e}\right)^{1,5} \end{aligned}\end{split}\]

with:

Variable	Description	Units
Q1	Discharge through WEIR	m3/s
C	Discharge coefficient
B	width of the threshold	m
H1	head upstream	m
He	edge level	m

The first equation is only valid if the downstream head, H2, is lower than the flush criterion head and the upstream head is greater than the edge level:

(4.38.2)\[H_{2}-H_{\mathrm{e}} \leq \frac{2}{3}\left(H_{1}-H_{\mathrm{e}}\right)\]

(4.38.3)\[H_{1} \geq H_{\mathrm{e}}\]

and

(4.38.4)\[H_1 \geq H_2\]

in which H₂ is the head downstream of the weir [m].

If expression (4.38.2) is violated, a warning is issued. In this case the weir behaves like a flush or submerged weir (Fig. 4.38.3) and equation (4.38.1) is no longer valid.

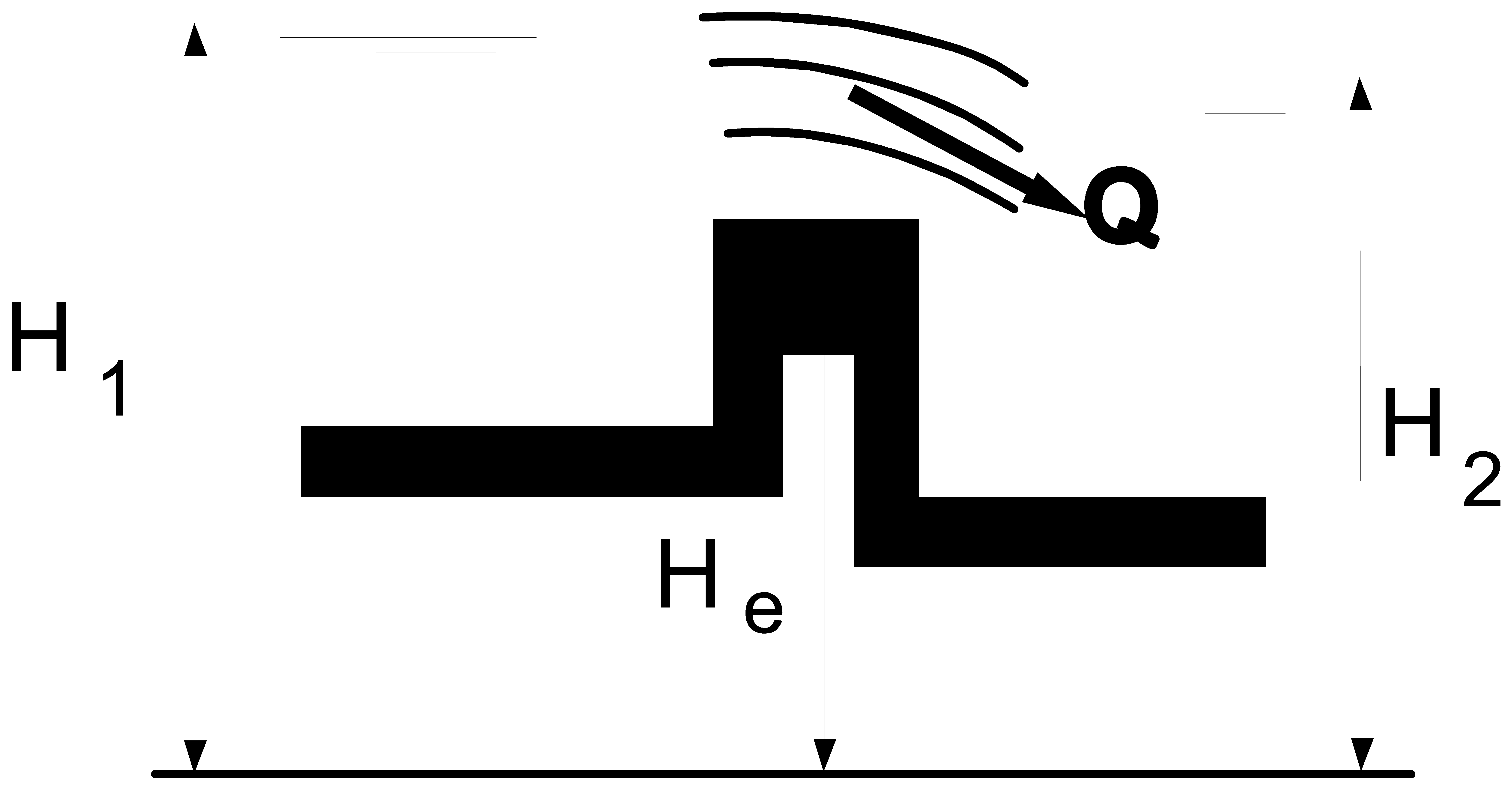
Fig. 4.38.3 Flush flow over a weir

If the weir is submerged and , the flow is no longer influenced by the weir. This situation should therefore be avoided. For a submerged weir the following equations describe the behaviour:

(4.38.5)\[F_1: Q=B C\left(H_{2}-H_{\mathrm{e}}\right) \sqrt{2 g\left(H_{1}-H_{2}\right)}\]

If expression (4) is violated, i.e. the downstream head is larger than the upstream head. The WEIR can cope with this situation and will have a discharge in negative direction. This component can be modelled by the following equations if the negative flow over the edge is critical.

(4.38.6)\[F_1: Q = -1.7 BC \left( H_2 - H_2 \right)^{\frac{3}{2}}\]

This flow is critical if the upstream head is lower than the flush criterion head and the downstream head is greater than the edge level:

(4.38.7)\[H_1 - H_2 \leq \frac{2}{3}\left(H_2 - H_e\right)\]

(4.38.8)\[H2 \geq H_e\]

and

(4.38.9)\[H_2 \geq H_1\]

If expression (4.38.7) is violated, a message is issued. In this case the weir behaves like a flush or submerged weir. If the weir is submerged, the flow is no longer influenced by the weir. For a submerged weir with negative flow equation (4.38.6) is no longer valid. In that case the following equations are describing the behaviour:

(4.38.10)\[F_1 : Q = BC\left(H_1 - H_e\right)\sqrt{2g\left( H_2 - H_1 \right)}\]

If expression \(H_1 \geq H_e\) and \(H_2 \geq H_e\) are violated the weir runs dry (‘closes’), thus if H₁ < H_e then

(4.38.11)\[F_1 : Q_1 = 0\]

Or verbatim: there is no discharge over the weir.

In steady state the weir can be ‘open’ (H₁ > H_e or H₂ > H_e) or ‘closed’ (H₁ <= H_e or H₂ <= H_e).

Whether the weir is open or closed depends on the hydraulic state of the total system. In steady state the user must initialise the initial state of the weir (critical, submerged or closed). The program does not calculate the initial state automatically.

4.38.1.2. Discharge coefficient

Broad crested weirs

According to the literature the coefficient C in equations 1 and 2 is the product of two separate coefficients: The approach velocity coefficient Cv which corrects for the velocity upstream of the weir, and the Discharge coefficient Cd which corrects for the energy losses that occur at the weir:

(4.38.12)\[C=C_{v} \cdot C_{D}\]

The discharge coefficient must be obtained through calibration of the weir. If the discharge coefficient is unknown, an estimate can be obtained with the following equations.

The approach velocity coefficient is given by:

(4.38.13)\[C_{v}=\left(\frac{H_{1}}{h_{1}}\right)^{1,5}=\left(1+\frac{v_{1}^{2}}{2 g h_{1}}\right)^{1,5}\]

The water depth and velocity of the approach flow are unknown to Wanda, which means that the calculation of the approach velocity coefficient must be done by the user.

The discharge coefficient Cd corrects for the assumptions made for equation 1.

The figure below shows the relation between the ratio H1/L (the head upstream of the weir and the length of the weir) and the discharge coefficient.

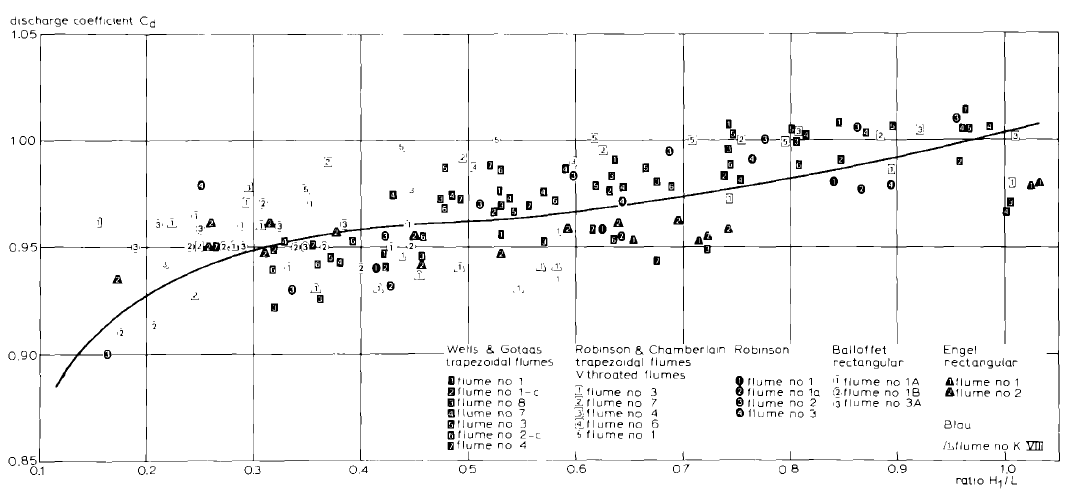
Fig. 4.38.4 Discharge coefficient as function of \(H_1/L\)

Short crested weirs

Short or sharp crested weirs are used for flowrate measurements in open channels. ISO 1438/1-1980 presents the following equation:

(4.38.14)\[Q=C \cdot \frac{2}{3} \sqrt{2 g} \cdot b \cdot\left(h_{1}+\frac{v_{1}^{2}}{2 g}\right)^{3 / 2}=C \cdot \frac{2}{3} \sqrt{2 g} \cdot b \cdot H_{1}^{3 / 2}\]

With:

Variable	Description	Units
Q	flow over the weir	[m3/s]
C	Discharge coefficient	[-]
b	width of the weir	[m]
H1	Head upstream of the weir	[m]
g	gravitational acceleration	[m/s2]

According to ISO, the discharge coefficient is given by the following equation:

(4.38.15)\[C=0,627+0,018\left(\frac{H_{1}}{p}\right)^{3 / 2}\]

with:

Variable	Description	Units
\(H_1\)	Head upstream of the weir	m
p	height of the weir	m

The following figure illustrates the different parameters

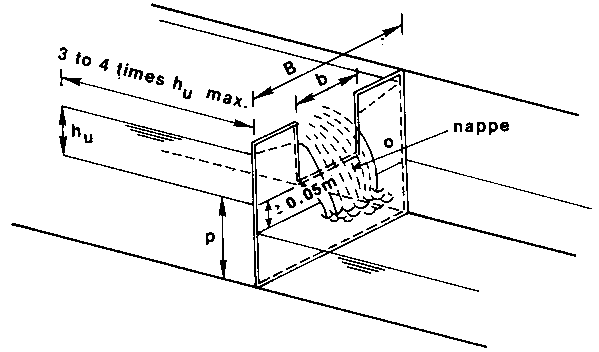
Fig. 4.38.5 Schematized weir showing the parameters that define the discharge coefficient.

The ISO equation for the discharge over the weir is not the same as the equation that Wanda uses, but this can be compensated with the discharge coefficient. To model the ISO-compliant weir in Wanda we need to use the following equation for the discharge coefficient C:

(4.38.16)\[C_{\text {Wanda }}=1.732 \cdot\left(0,627+0,018\left(\frac{H_{1}}{p}\right)^{3 / 2}\right)\]

Wanda cannot solve this equation because the water depth upstream of the weir (and thus p) is unknown.

References

• Bos, M.G. “The Use of Long-Throated Flumes to Measure flows in Irrigation and Drainage canals” Agricultural Water Management, 1 (1977) p111-126.

• Boiten, W. “Flow measurement structures” Flow measurement and Instrumentation, 13 (2002) pag. 203-207

• International Standards Organization (ISO), “Water flow measurement in open channels using weirs and venturi flumes” International Standard ISO 1438/1-1980, 1980.

4.38.2. WEIR (two way)

4.38.2.1. Hydraulic specifications

description	Input	Unit	range	default	remarks
edge level	Real	[m]
width	Real	[m]	(0-1000]
discharge coefficient	real	[-]	(0-2]
discharge coeff. (Q<0)	real	[-]	(0-2]
initial state	critical / submerged/ closed / crit. Q<0/ subm. Q<0			critical	Q<0

It is preferable to take an initial state of the WEIR in the steady state with a discharge in positive direction or closed.

The WEIR does not model the storage of the weir. To model both the up- and downstream storage of the WEIR, three discharges should be known. The discharge entering and leaving the WEIR are necessary to determine how much fluid stays in the storage of the WEIR. The discharge over the edge of the WEIR is necessary to determine how this fluid is divided over the up- and downstream storage. Only two of these variables can be known to Wanda, therefore it is impossible to model the storage both up- and downstream of the WEIR. It is left to the user to, if necessary, model the storage using a surge tower up- and downstream of the WEIR.

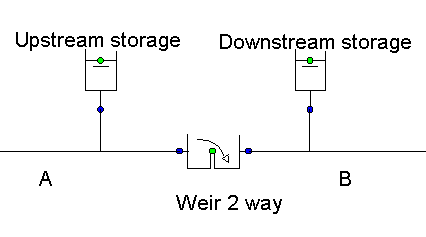
Fig. 4.38.6 Schematic model of a weir with storage.

See also “WEIR” (Section 4.38.1).

4.38.2.2. Component specific output

None

4.38.2.3. H-actions

None

4.38.2.4. Component messages

Message	Type	Explanation
starts in critical state	Info
starts in submerged state	Info
starts in closed state	Info
enters critical state	Info
enters submerged state	Info
closes	Info
enters critical state, neg. flow	Info
enters submerged state, neg. flow	Info

4.38.3. WEIR_S (class)

Fig. 4.38.7 Weir

Supplier type

type label	description	active
Outlet WEIR (incl. storage)	Broad-crested weir, only capable of simulating discharge in positive direction. Storage upstream of the weir is modelled.	No

4.38.3.1. Mathematical model

The component weir_S is often used in sewage water systems. The WEIR_S can have a discharge in positive direction or be closed. If the upstream head, H1, is larger than the edge of the WEIR_S, He, then the WEIR_S will have a discharge in positive direction. The component can be modelled by the following equations if the flow over the edge is critical (see Fig. 4.38.8):

(4.38.17)\[Q=1.7 \cdot B C\left(H_{1}-H_{\mathrm{e}}\right)^{3 / 2}\]

with:

Variable	Description	Units
Q	Discharge through WEIR	m3/s
C	Discharge coefficient	m1/2/s
B	width of the threshold	m
H1	head upstream	m
He	edge level	m

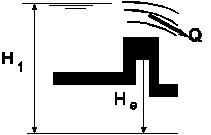
Fig. 4.38.8 Critical flow over a weir

For more information about the discharge coefficient see “Discharge coefficient” ():numref:sec_weir_discharge_coefficient).

4.38.4. Outlet WEIR (incl. storage)

4.38.4.1. Hydraulic specifications

description	Input	Unit	range	default	remarks
edge level	Real	[m]
width	Real	[m]	(0-1000]
discharge coefficient	real	[-]	(0-2]
Area upstream storage		[m2]	(0.001-500]
initial state	critical/ dry			critical

The WEIR_S (with storage) is a one way weir with critical flow only. The storage upstream of the weir is modelled. This weir can only be used as boundary condition in a system.

For outlet structure the WEIR_S can be used Instead of the combination Surge tower – Weir (2-way) – Boundh;

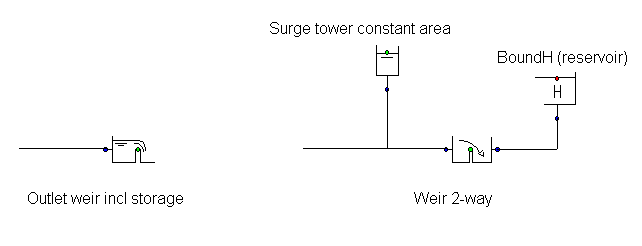
Fig. 4.38.9 Schematic representation of the outlet weir

See also “WEIR_S (class)” (Section 4.38.3).

4.38.4.2. Component specific output

Fluid level [m]

Discharge about weir [m³/s]

4.38.4.3. H-actions

None

4.38.4.4. Component messages

Message	Type	Explanation
starts in critical state	Info
starts in dry state	Info
enters critical state	Info
Enter dry state	Info